Sejam , e vetores não nulos. Faça o que se pede:
- Partindo o item “a)”, represente geometricamente .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá três vetores não nulos e nos pede para fazer o esboço de , a partir do que descobrimos no item a).
Lembrando que no item a), temos:

Assim, para descobrirmos , temos que saber do que é um produto escalar, um produto vetorial e o módulo de dois vetores.
O produto vetorial é descrito da seguinte forma:
“Dados dois vetores independentes linearmente e , o produto vetorial é um vetor perpendicular ao vetor e ao vetor e é a normal do plano contendo os dois vetores.”
O produto escalar é descrito assim:
“trata-se da multiplicação entre dois vetores que tem como resultado uma grandeza escalar. Ele associa a dois vetores um número real.”
E o módulo trata-se apenas do tamanho desse vetor.
Não entendeu? Então bora junto 😉
Passo 2
Bom... fazendo o esboço de acordo com o que foi apresentado no Passo 1, temos:
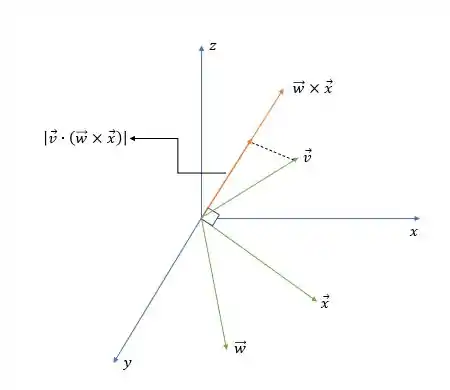
Entendeu direitinho? Responde aee ;)

Resposta
Ei, a resposta está no passo a passo :)