O campo elétrico de uma onda eletromagnética plana e monocromática que se propaga no vácuo é descrito por
onde , e são constantes positivas. Em função dos dados do enunciado e de constantes fundamentais, calcule o que se pede, justificando os cálculos.
a) Determine o comprimento de onda, o período de oscilação e a direção e o sentido de propagação dessa onda.
b) Determine a polarização da onda.
c) Determine o vetor campo magnético (módulo, direção e sentido) dessa onda eletromagnética.
Passo 1
Eai galerinha, bora resolver essa questão sobre ondas eletromagnéticas?
O problema deu para gente um campo elétrico:
Nota-se que as componentes do campo elétrico estão nas direções e , isto é, o vetor campo elétrico está no plano . Além disso, o argumento das funções trigonométricas é , o que sugere que a onda se propaga na direção positiva do eixo .
Para achar o período , nós lembramos que a frequência angular é dada por
Fazemos o mesmo para achar o comprimento de onda dado que o número de onda é dado por
Esse foi o item (a), bem tranquilo né?
Passo 2
Agora vamos para o item (b). Queremos determinar a polarização da onda!
Aqui você precisa saber de uma coisa: a polarização da onda corresponde a direção que o vetor campo elétrico oscila. Para a gente analisar isso, vamos olhar para as componentes do campo elétrico:
É fácil perceber que
Isso significa que o vetor campo elétrico está preso num círculo de raio . Trata-se, portanto, de uma polarização circular! Para a gente verificar o sentido da polarização, vamos considerar a posição :
Com isso, podemos marcar o vetor para os instantes de tempo: , , e , onde é o período. Lembrando que
Com isso, achamos:
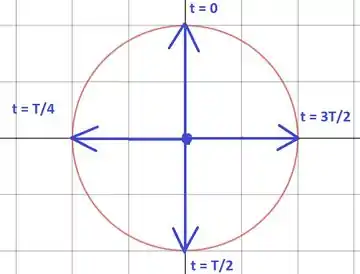
É fácil perceber que o vetor está girando no sentido anti-horário. Portanto, trata-se de uma polarização circular anti-horária.
Passo 3
No último item queremos achar o campo elétrico correspondente. Para isso, usaremos a Lei de Faraday na forma diferencial:
O primeiro passo é calcular o rotacional do campo elétrico:
Mas note que os campos não dependem de e , apenas de . Desta forma, podemos desprezar as derivadas e . Além disso, , de modo que
Como , temos que
E, usando , achamos
Logo,
Passo 4
Com isso, temos que
Agora temos que integrar com relação ao tempo:
Com isso, temos que
Lembrando que e jogando o sinal para dentro:
Uma coisa legal da gente observar é que
Isso significa que mesmo na polarização circular, os vetores e são perpendiculares! Poderíamos calcular também o vetor de Poynting, que claramente daria na direção (direção de propagação da onda), como deve ser!
Resposta
Polarização circular anti-horária.