Uma onda eletromagnética monocromática, viajando no sentido no vácuo, tem polarização circular direita e comprimento de onda igual a . Na origem e em o campo elétrico tem amplitude máxima dada por .
a) Escreve a expressão para o campo elétrico dessa onda, em função do tempo e espaço.
b) Encontre o campo magnético através da Lei de Faraday. Verifique a sua resposta através de .
c) Descreva duas maneiras de transformar o estado de polarização dessa onda para polarização linear.
Passo 1
Eai galerinha, bora resolver mais uma questão de física 4!
Nesse problema vamos discutir um pouquinho sobre polarização circular! Vale lembrar que a polarização nada mais é do que a direção do campo elétrico na onda eletromagnética.
Como a polarização é circular e a onda se propaga na direção , o vetor deve estar no plano :
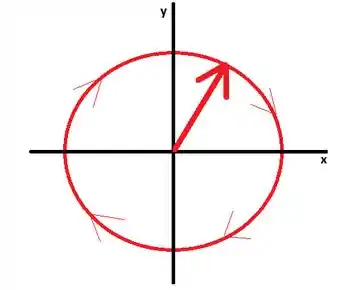
Como a polarização circular é à direita, o vetor deve varrer o círculo no sentido horário. Para isso, escrevemos
Se a polarização fosse à esquerda, teríamos que inverter a componente com a . Para achar e , usamos que para e ,
Assim,
Basta escolher e . Portanto,
Passo 2
Para achar e , usamos
Assim, achamos
Se você quiser calcular e numericamente sinta-se a vontade, mas acho que a resposta fica mais elegante dessa forma!
Passo 3
No item (b) queremos achar o campo usando a lei de Faraday:
Primeiro calculamos o rotacional:
Como e as demais componentes não dependem de e , podemos escrever
Agora calculamos as derivadas:
Logo,
Usando a lei de Faraday:
Passo 4
Daí é só integrar no tempo:
Fazendo as integrais, achamos
Usando que , temos que
Observe que
Isso significa que os campos são perpendiculares, como devem ser! Além disso,
Como e , temos que
Logo,
Portanto, o campo que achamos concorda com a expressão geral fornecida no enunciado!
Passo 5
Para terminar o problema, vamos resolver o item (c)!
Ele quer saber como podemos transformar uma onda circularmente polarizada em uma onda linearmente polarizada.
Uma das formas de se fazer isso é fazendo com que a onde seja refletida por uma superfície com o ângulo de Brewster. Sempre que uma onda com polarização qualquer incide sobre uma superfície plana que separa dois meios com o ângulo de incidência sendo igual ao ângulo de Brewster, a onda refletida tem polarização linear perpendicular ao plano de incidência.
Com isso, uma das formas de obter a onda linearmente polarizada é refletir uma onda circularmente polarizada com incidência igual ao ângulo de Brewster.
Uma outra forma de se fazer isso é fazer com que a luz circularmente polarizada atravesse um polarizador linear. Lembre-se que podemos decompor a onda circularmente polarizada em duas componentes que oscilam harmonicamente e estejam defasadas em (uma seja um seno e a outra seja um cosseno). Se a luz atravessa um polarizador linear, uma dessas componentes é anulas e a outra atravessa e a polarização da onda transmitida passa a ser linear.