Obtenha a polarização da onda eletromagnética representada abaixo. Demonstre o tipo de polarização (linear, circular ou elíptica) e mostre, caso não seja linear, se a polarização é à esquerda ou à direita. Use a técnica vetorial usada em aula:
onde .
Passo 1
Para determinar o tipo de polarização, precisamos avaliar se as componentes do vetor campo elétrico tem a mesma amplitude e precisamos também determinar se há diferença de fase entre as componentes, e de quanto é essa diferença.
Passo 2
Para vermos a diferença de fase das duas componentes do campo elétrico, o melhor é escrevermos elas como uma mesma função trigonométrica. A trigonometria nos diz que:
Se , temos:
Como a compontente tem um seno podemos rescrever essa parte como
Assim:
Agora dá pra comparar! A diferença de fase vai ser:
A polarização será circular ou será elíptica.
Passo 3
Para determinar se a polarização é circular ou elíptica, devemos avaliar se as amplitudes de cada componente são iguais ou diferentes. Pela informação dada, vemos que as amplitudes são diferentes, pois:
Então temos uma polarização elíptica
Passo 4
Para determinar o sentido da polarização, precisamos calcular o vetor campo elétrico, que é a soma das componentes, para dois instantes no tempo, para e para , do ponto de observação . Sabendo que , temos que , ou seja, .
Para e , temos:
Ou seja, para e , temos que o vetor campo elétrico é:
Para e , temos:
Ou seja, para e , temos que o vetor campo elétrico é:
Passo 5
Para determinar a direção do giro vamos fazer um desenho do campo elétrico em nos dois tempos que calculamos acima, ou seja
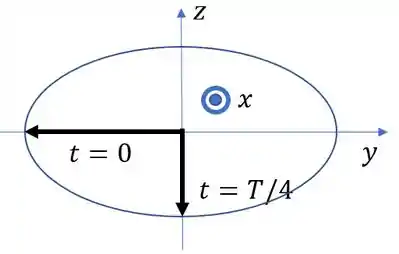
Aqui eu supus , mas podia ser o contrário!
Como a onda está se propagando na direção (pois o argumento do lá das funções trigonométricas é ), então para um observador que vê a onda vir na sua direção a direção da polarização é anti-horária como tá no nosso desenho!
Resposta
A polarização é elíptica e, para um observador que vê a onda vir na sua direção, a direção da polarização é anti-horária.