Em certa região do espaço, o campo magnético de um feixe luminoso é dado por

em unidades do SI.

Encontre a frequência angular e o comprimento de onda associados.

Ache o vetor campo elétrico por aplicação da Lei de Àmpere. Confira sua resposta

usando  .

Diga qual é o estado de polarização da luz, justificando.

Esse feixe luminoso incide perpendicularmente sobre um aparato de fenda dupla, tal que as fendas têm abertura desprezível e estão separadas de . A fenda superior (ver

figura) está coberta por uma fina lâmina cujo índice de refração é e tem espessura de .

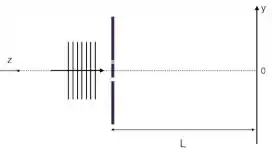
Logo após a saída das fendas, qual é a diferença de fase entre raios paralelos emergindo das fendas superior e inferior?

Em uma tela posicionada a do aparato, em que posição estará o máximo (deslocado) de ordem zero?

Item .

Esse quer na verdade o comprimento de onda e a frequência angular do campo magnético que está dado na forma de uma função de onda da seguinte forma:

Ou

Comparando com o que temos vemos que:

Podemos encontrar o comprimento de onda usando a seguinte equação:

E a frequência angular da seguinte maneira:

Vamos então encontrar e .

Começando com , temos:

Agora vamos achar , temos:

Prontinho, menos um para conta!

Item .

Para encontrar o vetor campo elétrico pedido nesse item, teremos que usar a lei de Àmpere como já diz o enunciado. A lei de Àmpere para esse caso é dada por:

Então para achar primeiro vamos calcular o rotacional de depois vamos integrar toda a expressão em fu8nção do tempo. Vamos lá!

Como o campo só tem componentes na direção e que dependem de , só nos sobra o seguinte:

Agora vamos calcular essas derivadas, temos:

Então temos que:

Então temos que:

Então agora precisamos integrar os dois lados da equação em função de , assim:

Integrando, ficamos com:

Item .

Esse item quer saber a polarização da luz. Então é bom termos calculado o campo elétrico já que a polarização da luz é dada com base na direção do campo elétrico.

O campo elétrico que encontramos é dado por:

Como você pode ver ele tem duas componentes uma na direção positiva de e uma na direção negativa de .

Com base nisso podemos dizer que o vetor campo elétrico tem uma inclinação que pode ser representado com a seguinte figura:

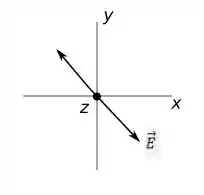
Assim temos que a polarização da luz tem direção oblíqua.

Item .

Para encontrar a diferença de fase das duas ondas depois da fenda basta calcularmos a diferença entre o número de comprimentos de onda que passa pela película e o que não passa pela película.

Isso é dado pela seguinte equação:

Onde é o comprimento da película e é o índice de refração da película e do ar.

Fazendo essa conta encontramos a diferença de fase em termos de comprimento de onda. Vamos lá então, temos:

Agora para encontrarmos esse valor em radianos temos que lembrar que comprimento de onda equivale a , então fazendo uma regrinha de três, temos que:

Essa é a diferença de faze.

Item .

Esse item quer saber a nova posição do máximo central devido a película na fenda superior.

Para isso temos que notar que o acréscimo da película causa uma diferença de caminho no percurso dos raios, essa diferença é dada por:

E essa diferença tem que ser um múltiplo inteiro do comprimento de onda para que tenhamos interferência construtiva.

Mas temos que lembrar da diferença de caminho natural do percurso depois da película que é dada por:

Que também tem que ser um múltiplo inteiro do comprimento de onda. Então para que tenhamos a interferência, temos que:

Mas queremos a posição do máximo, para isso temos que lembrar que para pequenos ângulos, temos que:

Com isso temos que:

Então vamos calcular essa posição. Como ele quer o máximo de ordem zero, temos que , assim:

Substituindo os valores que conhecemos, temos: