Obtenha a polarização da onda eletromagnética representada abaixo. Demonstre o tipo de polarização (linear, circular ou elíptica) e mostre, caso não seja linear, se a polarização é à esquerda ou à direita. Use a técnica vetorial usada em aula:
, onde .
Passo 1
Para determinar o tipo de polarização, precisamos avaliar se as componentes do vetor campo elétrico tem a mesma amplitude e precisamos também determinar se há diferença de fase entre as componentes, e de quanto é a diferença.
Passo 2
Dadas as duas componentes do campo elétrico polarizado, podemos perceber que há uma diferença de fase de , como vemos pela adição de ao argumento do ângulo em .
Por se tratar de uma diferença de fase, podemos concluir que a polarização não é linear, podendo ser circular ou elíptica.
Passo 3
Para determinar o tipo de polarização entre circular ou elíptica, devemos avaliar se a amplitude das componentes é a mesma ou se é diferente. Pela informação dada, vemos que as amplitudes são diferentes, pois temos:
Desse modo, determinamos que se trata de uma polarização elíptica
Passo 4
Para determinar o sentido da polarização, precisamos calcular o vetor campo elétrico, que é a soma das componentes, para dois instantes no tempo, para e para , do ponto de observação . Sabendo que , temos que , ou seja, .
Para , temos:
Ou seja, para e , temos que o vetor campo elétrico é:
Para , temos:
Ou seja, para e , temos que o vetor campo elétrico é:
Passo 5
Para determinar a direção do giro, devemos utilizar a seguinte regra, apontando o dedão no sentido de propagação da onda, perpendicular ao plano dado, devemos determinar que mão possui os dedos restantes apontando o sentido de giro do vetor campo elétrico, bem parecido com a regra da mão direita, só que agora podemos utilizar ambas as mãos.
Parece complicado, mas vamos analisar o caso dado:
Apontando o dedão para fora do papel, vemos que somente a mão esquerda possui os dedos apontando no sentido do giro do vetor campo elétrico, tendo em vista que o campo elétrico passa de para em um quarto do período. Ou seja utilizamos a mão esquerda, e portanto, temos que a polarização é elíptica à esquerda. Veja que com a mão direita, vamos no sentido contrário, de para !
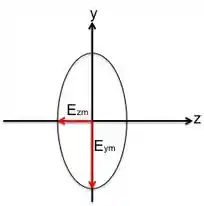
Resposta
A polarização é elíptica à esquerda.