O campo elétrico de uma onda plana eletromagnética monocromática no vácuo é dado por
- Obtenha a expressão para o campo magnético associado a essa onda.
- Discuta a evolução no tempo do campo elétrico na posição , por meio de um esboço de no plano de polarização. Que tipo de polarização esta onda apresenta?
- Determine a média temporal do vetor de Poynting .
- Considere uma bactéria de estrutura esférica de raio e massa que absorve completamente a radiação eletromagnética que a atinge (e não reflete), de baixo para cima.
Desprezando outros possíveis efeitos, determine o valor mínimo de para que a bactéria não caia sob o efeito da gravidade, se a onda plana aqui discutida for usada para suspendê-la (suponha que a superfície de absorção da bactéria seja um disco de raio ).
Passo 1
Letra a)
O produto vetorial de e sempre vai apontar no sentido de propagação da onda .Além disso, como eles são perpendiculares, o produto vetorial entre e também vai apontar no sentido do campo magnético .
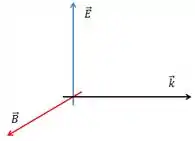
Além disso, é unitário e os módulos do campo elétrico e magnético se relacionam por:
Podemos então achar o campo magnético fazendo o seguinte produto:
Uma forma de lembrar o produto vetorial é pelo seguinte determinante:
Como a onda se propaga ao longo do eixo (pois é a variável que aparece no argumento do campo elétrico), então e . Além disso, no vetor campo elétrico, .
E então, temos:
Passo 2
Letra b)
Na posição , temos . Agora vamos ver como esse campo elétrico varia no tempo.
O período do seno e do cosseno é de , e assim vamos dividir esse tempo em quatro intervalos e avaliar a evolução do campo elétrico.
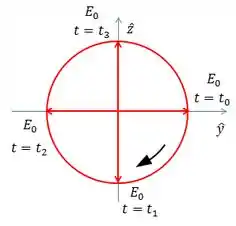
Essa onda apresenta polarização circular, girando no sentido horário pra quem olha no sentido negativo do eixo !
Outra forma de vermos isso é colocando as duas componentes como uma mesma função trigonométrica para vermos sua diferença de fase.
Essa diferença entre elas vai ser:
A regra é que quando e as amplitudes são iguais temos uma polarização circular!
Passo 3
Letra c)
O vetor de Poynting é dado por:
Como , teremos:
Como o módulo do vetor de Poynting é sempre constante e igual a , quando fizermos sua média no tempo, ela vai dar esse mesmo valor.
A média temporal do vetor de Poynting é a intensidade luminosa. Então neste caso:
Mas por que não aparece um fator no denominador?
Quando esse fator aparece, é porque o vetor de Poynting varia com o tempo! Quando ele varia como um seno ou cosseno, a sua média é a sua amplitude dividida por dois.
Mas nesse caso, temos a média de um valor constante, que é o próprio valor.
Passo 4
Letra d)
Como a bactéria absorve toda a radiação incidente, a pressão exercida sobre ela vai ser:
Pela discussão anterior, essa pressão vai ser então:
A força exercida vai ser a pressão multiplicada pela área da superfície de absorção.
Pelo enunciado, a área é um disco de raio , e por isso vai ser dada por:
Essa força tem que contrabalancear a força gravitacional que atua na bactéria, e por isso:
Podemos substituir a equação anterior, e rearrumar o resultado para achar o valor necessário da magnitude do campo elétrico.
Resposta
Letra a)
Letra b)
Polarização Circular
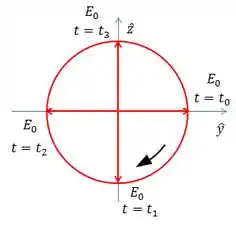
Letra c)
Letra d)