Origem do Exercício
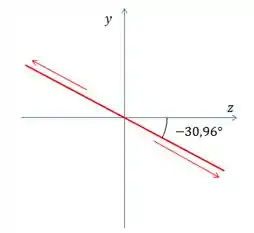
– Obtenha a polarização da onda eletromagnética representada abaixo. Demonstre o tipo de polarização (linear, circular ou elíptica) e demonstre, caso não seja linear, se a polarização é à esquerda ou à direita.
Caso seja linear obtenha o ângulo de inclinação da reta entre os componentes e e faça um desenho dessa polarização no eixo :
; , onde .
Passo 1
Primeiro, vamos analisar as componentes do campo elétrico.
Ambas são representadas pela função seno. Assim, para saber a diferença de fase entre elas, basta subtrairmos o que está dentro da função.
Quando a defasagem é de , a polarização é linear, independente das amplitudes de e .
Passo 2
Podemos observar que a polarização de fato é linear mostrando que as duas componentes seguem a equação de uma reta.
Para isso, vamos usar que:
Além do fato de que e , o que nos dá:
Com isso, podemos ver que:
Que é a equação de uma reta com coeficiente linear zero.
Nessa reta, o coeficiente angular é:
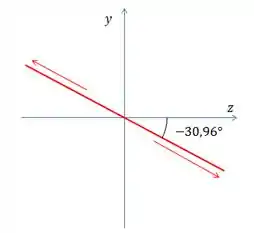
Resposta
A polarização é linear e o ângulo que a reta faz com o eixo é .
