Considere agora que esse feixe tem seu campo elétrico representado pela expressão
onde os eixos cartesianos estão orientados como mostrado na figura. Observa-se que, para determinado ângulo de incidência, o feixe de luz após reflexão (feixe emergente em 2) está linearmente polarizado.
(b) Qual é o estado de polarização do feixe incidente? Justifique.
(c) Qual é a direção de polarização do feixe refletido? Justifique.
(d) Qual é o ângulo de incidência para o qual esse efeito ocorre?
Passo 1
Nesse caso queremos determinar o estado de polarização do feixe incidente, para isso temos que lembrar que ele então quer que definamos se a luz é linearmente polarizada( ou se ela é circularmente/ elipticamente polarizada (, caso seja a segunda opção, ainda temos que definir se é para a esquerda ou para direita caso seja o ultimo caso. Então vamos lá.
Passo 2
Se o nosso campo é
De cara vemos que ele possui uma componente Seno e outra Cosseno, logo eles possuem uma diferença de fase de , causado exatamente pelo fato do seno e cosseno serem a 90° um do outro, como não temos mais nenhuma diferença de fase no argumento dos termos concluímos que a polarização é circular ou elíptica. Como a amplitude de ambas as componentes é , então essa onda é circularmente polarizada.
Agora para saber o lado de polarização basta fazer a analise para 2 estados.
Um para o caso de
E outro para
Mas sabemos que
Substituindo
Passo 3
Vamos fazer a analise
X=0 e t=0
A segunda analise será
X=0 e
Testando as duas mãos girando em torno do encontro dos eixos, a que girar no sentido de rotação do vetor será a resposta.
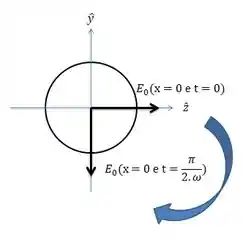
Nesse caso a rotação é segundo a mão esquerda, logo a luz é circularmente polarizada a esquerda.
Passo 4
Agora o nosso objetivo é determinar a direção de polarização do eixe refletido, e devemos pensar da seguinte maneira, se o feixe refletido saiu linearmente polarizado significa que ocorreu algo como indicado na figura.
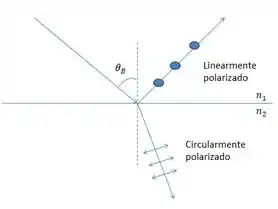
Se isso ocorreu, então o ângulo de incidência é o que chamamos de ângulo de Brewster que é dado pela fórmula
Quando isso ocorre, sabemos que a direção de polarização é perpendicular ao plano de incidência, como no item a, descobrimos que o plano de incidência é xy então a polarização linear está na direção z, que é perpendicular ao plano de incidência.
Passo 5
Como foi dito no item anterior, para que essa polarização aconteça o nosso ângulo de incidência respeita a fórmula de Brewster que garante que , logo junto com a lei de Snell concluímos que
Resposta
- circularmente polarizada a esquerda.
- polarização linear está na direção z