– Obtenha a polarização da onda eletromagnética representada abaixo.
Demonstre o tipo de polarização (linear, circular ou elíptica) e mostre, caso não seja linear, se a polarização é à esquerda ou à direita através da técnica usada em aula:
; , onde .
Passo 1
Para sabermos qual a polarização da onda, primeiros temos que saber sua defasagem.
Mas as suas componentes estão com um seno e coseno, o que dificulta que vejamos a diferença de fase facilmente. Então, vamos tentar colocar as duas como coseno ou como seno.
Para isso, podemos usar uma fórmula que às vezes se encontra na prova:
Usando isso em , e lembrando que e , temos:
O sinal muda apenas o sentido da componente. E com isso, vemos que a diferença de fase entre as duas é de , pois é a diferença dos argumentos dentro do coseno.
Passo 2
Como a diferença de fase é de e as amplitudes são diferentes , então sabemos que a polarização é elíptica.
Além disso, graças a essa diferença de fase, a elipse que a onda descreve não é inclinada em relação aos nossos eixos. Por isso, podemos tentar escrever a equação da elipse com as duas componentes.
A equação de uma elipse é:
No nosso caso, vamos usar e invés do , por causa das nossas componentes. Mas vamos com calma.
Para acharmos essa equação, precisamos ainda mudar o de forma semelhante ao passo anterior. A outra relação que costuma ter em prova vem aí!
Com isso:
Por fim, usando e e teremos:
Que é a nossa equação da elipse! Ou seja, de fato a nossa onda é elipticamente polarizada.
Passo 3
Agora falta descobrirmos se a polarização é à esquerda ou à direita. Isso é uma convenção baseada no sentido de rotação, que não é uma convenção.
Vejamos o sentido de rotação dela, lembrando que ela se propaga no sentido positivo do eixo . (por causa dos sinais dentro das funções).
Primeiro, vejamos qual é o vetor campo elétrico para no tempo .

E pra onde ela gira a medida que o tempo passa? Para facilitar as contas, vamos usar um tempo em um quarto do giro, , onde é o período da rotação.
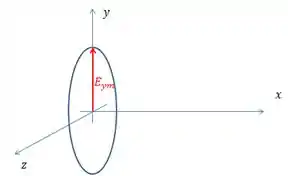
Olhando os gráficos, vemos que a polarização é anti-horária em relação ao sentido de propagação. Agora a convenção é a seguinte:
Coloque o dedão de cada uma das suas duas mãos no sentido de propagação da onda (sentido positivo do eixo ). A mão cuja palma você bater na direção do giro é a mão da rotação!
No caso, seria a mão direita, então ela é elíptica à direita!
Mas como eu falei isso é uma convenção (no caso, é a adotada pelo instituto de engenharia elétrica e eletrônica, IEEE). Por isso, se sua convenção é diferente, não me mate!
A outra convenção possível, que é frequentemente usada em livros de física (no livro do Moysés, por exemplo) é você fazer a mesma coisa, mas apontando no sentido contrário do sentido de propagação da onda. (é como se você apontasse pra fonte da onda). Nesse caso, você encontraria que a onda é elíptica à esquerda!
Então não falte todas as aulas de física 4. Vá, PELO MENOS, na aula onde seu professor define a convenção que ele usa! (O ideal é você ir em todas as aulas, mas eu entendo que às vezes você tem que levar a vó no Jiu Jitsu, o cachorro pegou fogo, coisas assim...)
Resposta
A polarização é elíptica à direita.
(Convenção IEEE)