– Obtenha a polarização da onda eletromagnética representada abaixo. Demonstre o tipo de polarização (linear, circular ou elíptica) e mostre, caso não seja linear, se a polarização é à esquerda ou à direita através da técnica usada em aula:

; , onde .

Podemos observar que a polarização de fato é elíptica mostrando que as duas componentes seguem a equação de uma elipse, que é:

Para isso, vamos usar que:

Além do fato de que e , o que nos dá:

Agora a equação da elipse se dá quando usarmos e .

Agora falta descobrirmos se a polarização é à esquerda ou à direita. Isso é uma convenção baseada no sentido de rotação, que não é uma convenção.

Vejamos o sentido de rotação dela, lembrando que ela se propaga no sentido positivo do eixo . (por causa dos sinais dentro das funções).

Primeiro, vejamos qual é o vetor campo elétrico para no tempo .

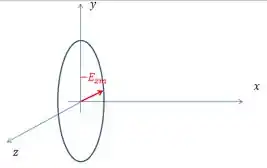
E pra onde ela gira a medida que o tempo passa? Para facilitar as contas, vamos usar um tempo em um quarto do giro, , onde é o período da rotação.

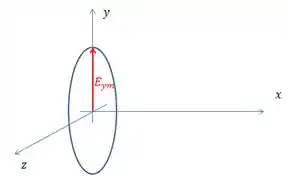
Olhando os gráficos, vemos que a polarização é anti-horária em relação ao sentido de propagação. Agora a convenção é a seguinte:

Coloque o dedão de cada uma das suas duas mãos no sentido de propagação da onda (sentido positivo do eixo ). A mão cuja palma você bater na direção do giro é a mão da rotação!

No caso, seria a mão direita, então ela é elíptica à direita!

Mas como eu falei isso é uma convenção. A outra convenção possível é você fazer a mesma coisa, mas apontando no sentido contrário do sentido de propagação da onda. (é como se você apontasse pra fonte da onda). Nesse caso, você encontraria que a onda é elíptica à esquerda!

Eu vou usar a primeira convenção, mas a convenção que você deve usar na prova é a que seu professor utiliza em aula!