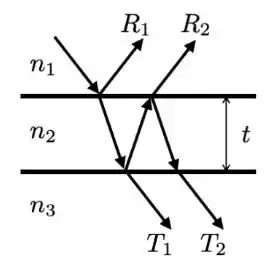
Um feixe de luz de frequência natural de ilumina um filme fino de largura , conforme a figura abaixo, na qual e .
Considere uma incidência normal.
Determine, em função dos dados do enunciado e substituindo todas as constantes pelos seus respectivos valores,
i) os comprimentos de onda da onda nos meios e ;
ii) a diferença de fase entre os raios e (indique claramente como cada raio ganha determinada fase e sua diferença); e
iii) o menor valor de (com ) para que os raios e se interfiram construtivamente.
Passo 1
Fala galerinha, essa é uma questão sobre interferência em filmes finos... bora lá?
Primeiramente queremos saber o comprimento de onda da onda nos meios e ...
Bom, sabemos que a velocidade da luz no meio é dada por:
E temos que:
Repare que a frequência da onda não se altera ao passar de um meio para outro, ela será sempre:
Dessa forma, temos que o comprimento será:
Passo 2
Bom, se considerarmos que a fase do raio é a nossa referência, teremos portanto que:
Já a fase do raio será maior que a do raio , devido ao caminho percorrido no meio somado a uma fase de reflexão que vale , dessa forma temos:
O comprimento de onda no meio 2 é dado por:
Substituindo, teremos:
Portanto, a diferença de fase entre os raios será de:
Passo 3
Por fim, para que os raios e se interfiram construtivamente, é necessário que a diferença de fase entre eles valha:
Substituindo o que encontramos, temos:
Cortando o ...
Para que seja maior que , ou seja:
É necessário que , pois, se , teremos:
Que é um índice que gera a interferência construtiva, no entanto, é menor que , o que não queremos, dessa forma, usando , teremos:
E esse é o menor índice de refração que gera a interferência construtiva.
Resposta
i)
ii)
iii)