Calcule o valor de .
Passo 1
Vamos lááá!! Aqui queremos calcular o valor de , certo?! Como vamos fazer isso então?
Se você reparar, esse ângulo é um ângulo que não está tabelado, certo?! O ideal aqui então para resolver esse exercício é tentar quebrar esse ângulo numa soma, subtração ou multiplicação de ângulos notáveis (tabelados). Beleza?!
Nesse caso aqui, podemos reescrever esse ângulo da seguinte forma
Note que agora temos o multiplicando um ângulo que temos o valor tabelado, então vamos utilizar isso a nosso favor!! Show de bola?!
Passo 2
Para calcular o precisamos utilizar a fórmula
Substituindo os valores, temos
E agora podemos substituir os valores da tabelinha que temos de ângulos notáveis
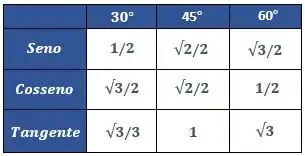
Assim, substituindo ficamos com
Portanto,
Show de bola?!
Resposta
Exercícios de Livros Relacionados
Calcule a soma dos 12 primeiros termos da série cos alpha , c o s (alpha + pi) , c o s (alpha + 2 pi) , ...
Sendo A do primeiro quadrante e arc sen x = A, ache arc cos x.
Resolva a equação:a r c t g ((1 + e^x)/(2)) + a r c t g ((1 - e^x)/(2)) = (pi)/(4)
Calcule t g (a r c s e n (3)/(4)) .
Prove as igualdades:a ) 2 a r c t g (2)/(3) + a r c cos (12)/(13) = (pi)/(2) b ) 3 a r c s e n (1)/(4) + a r c cos (11)/(16) = (pi)/(2)