Qual o valor de ?
Passo 1
Faaaala Aíí!! Como podemos encontrar o valor de ???
Podemos reescrever esse ângulo da seguinte forma:
Tá... Podemos... mas por que fizemos isso??
Se você reparar, conseguimos quebrar em uma soma entre dois ângulos notáveis (tabelados), concorda? Agora podemos resolver utilizando o seno da soma entre dois ângulos, que tem a seguinte carinha:
Beleza?!
Passo 2
Vamos então substituir os valores dos ângulos na fórmula
Show de bola?!
E agora podemos substituir os valores da tabelinha que temos de ângulos notáveis
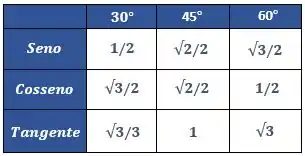
Assim, substituindo ficamos com
Agora é só partir pras continhas!!!
Show de bola?!
Resposta
Exercícios de Livros Relacionados
Calcule a soma dos 12 primeiros termos da série cos alpha , c o s (alpha + pi) , c o s (alpha + 2 pi) , ...
Sendo A do primeiro quadrante e arc sen x = A, ache arc cos x.
Resolva a equação:a r c t g ((1 + e^x)/(2)) + a r c t g ((1 - e^x)/(2)) = (pi)/(4)
Calcule t g (a r c s e n (3)/(4)) .
Prove as igualdades:a ) 2 a r c t g (2)/(3) + a r c cos (12)/(13) = (pi)/(2) b ) 3 a r c s e n (1)/(4) + a r c cos (11)/(16) = (pi)/(2)