Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Seno e Cosseno da Soma e Subtração de Arcos

Ver Teoria
Exercício 6123457891011121314151617

Enunciado

Qual o valor de t g 75 ° ?

Passo 1

Falaaa galeraaa!! Como podemos calcular a t a n g e n t e de um ângulo que não é notável, ou seja, não está tabelado?!

O ideal aqui é tentar quebrar esse ângulo numa soma, subtração ou multiplicação de ângulos notáveis (tabelados). Beleza?!

Nesse caso aqui, podemos reescrever esse ângulo da seguinte forma

t g 75 ° = t g 45 ° + 30 °

Onde os dois ângulos ( 45 ° e 30 ° ) estão na tabelinha de ângulos notáveis. Vamos então utilizar isso a nosso favor!!!

Passo 2

Para calcular o t g 45 ° + 30 ° precisamos utilizar a fórmula

t g a ± b = t g a ± t g b 1 ∓ t g a t g b

Substituindo os valores, temos

t g 45 ° + 30 ° = t g 45 ° + t g 30 ° 1 - t g 45 ° t g 30 °

E agora podemos substituir os valores da tabelinha que temos de ângulos notáveis

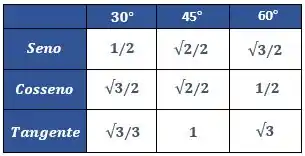
Assim, substituindo ficamos com

t g 45 ° + 30 ° = 1 + 3 3 1 - 1 ∙ 3 3

Portanto,

t g 75 ° = t g 45 ° + 30 ° = 1 + 3 3 1 - 3 3

Podemos dar aquela arrumadinha marota pra deixar a resposta de forma simplificada!! Colocando no mesmo denominador, temos

t g 45 ° + 30 ° = 1 + 3 3 1 - 3 3 = 3 + 3 3 3 - 3 3

Cortando os dois denominadores, temos

t g 45 ° + 30 ° = 3 + 3 3 - 3

Multiplicando o numerador e o denominador por 3 + 3 , temos

t g 45 ° + 30 ° = 3 + 3 3 - 3 ∙ 3 + 3 3 + 3

Fazendo a multiplicação

t g 45 ° + 30 ° = 12 + 6 3 6 = 2 + 3

Show de bola?!

Resposta

t g 7 5 ° = 2 + 3

Exercícios de Livros Relacionados

Calcule a soma dos 12 primeiros termos da série cos alpha , c o s (alpha + pi) , c o s (alpha + 2 pi) , ...
Sendo A do primeiro quadrante e arc sen x = A, ache arc cos x.
Resolva a equação:a r c t g ((1 + e^x)/(2)) + a r c t g ((1 - e^x)/(2)) = (pi)/(4)
Calcule t g (a r c s e n (3)/(4)) .
Prove as igualdades:a ) 2 a r c t g (2)/(3) + a r c cos (12)/(13) = (pi)/(2) b ) 3 a r c s e n (1)/(4) + a r c cos (11)/(16) = (pi)/(2)