Dada a função
a) Determine a série de Fourier de
b) Esboce o gráfico da série de Fourier de obtida no item (a) no intervalo .
c) Calcule a soma
Passo 1
a) Cara, para calcular essa extensão, a gente usa as fórmulinhas:
Como o intervalo da função que o problema deu tem tamanho (de até ) e temos que estender a função, esse será o seu período. Então:
Passo 2
Vamos calcular os coeficientes. Como a nossa função tem diferentes definições em diferentes intervalos, precisamos dividir as integrais em duas, uma para cada intervalo.
Fica assim:
Para
Como o formulário diz que
Temos que
O termo da esquerda zera, e ficamos com
E como a gente pode dizer que
Nosso coeficiente fica
Se for ímpar, temos
Mas se for par, temos
Passo 3
Vamos ao cálculo de .
O formulário diz para a gente que:
Aí nossa continha fica:
Como o cosseno é uma função par, temos que , aí ficamos com
Fazendo o que a gente fez no passo anterior, para valores pares de , temos:
Para valores ímpares:
Logo a nossa série será
Passo 4
b) Agora vamos esboçar o gráfico dessa função no intervalo .
O enunciado pede para desenharmos o gráfico da função para qual a série converge. Ah, é só desenhar a função do enunciado, né?
Não! O que você vai fazer nesse tipo de questão é o seguinte:
- Desenhar as informações sobre que o enunciado dá nos colchetes (em vermelho)
- Repetir essa para a esquerda e para a direita ignorando os pontos de descontinuidade (em azul); (já que queremos ir de até )
- Fazer a média dos limites laterais em cada ponto de descontinuidade (em preto)
Por que isso?
Por causa daquele Teorema da Convergência de Fourier que diz que a soma da série de Fourier de converge para onde a função é contínua (por isso nós copiamos essas retas do enunciado) e converge para a média dos limites laterais nos pontos de descontinuidade:
Para , a soma da série converge para:
E para :
Lembre-se de fazer pontos preenchidos quando representar essas médias (em preto) e pontos “vazios” (em azul e vermelho) nos limites laterais.
Portanto, esse gráfico que fizemos não representa , mas a soma da sua série de Fourier, ok? Claro que a soma da série é muito parecida com a função.
Estendendo esse gráfico de um período para trás e um período para a frente, nosso esboço fica assim:
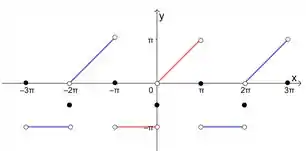
Passo 5
c) Vamos ter que brincar um pouco com a nossa função e a série de Fourier em um ponto, para chegarmos na expressão dessa soma.
Queremos chegar em
A gente pode ir lá na série que a gente calculou:
E tentar fazer , para ver no que dá
Temos que
Aí fazemos:
Passo 6
Vamos olhar cada termo desse com carinho. Vamos começar por
Para par ele alterna entre e , e para ímpar, ele zera. Mas repara que ele está em produto com o termo:
Que zera para valores de par. Temos então dois termos em produto. Um zera quando é ímpar e o outro quando é par, então esse termo todo vai zerar:
Daí tiramos que:
Passo 7
Vamos olhar agora para
Quando é par, esse cara zera, mas quando é ímpar, ele alterna entre e . A gente pode fazer então , porque aí só ficamos com os termos ímpares.
Agora vamos ver se esse expoente do está certo.
Mas repara que diz que em , . Então esse sinal está errado, a gente precisa mudar esse expoente. Para ficar parecido com a nossa soma, vamos fazer:
Nossa expressão fica:
Passo 8
Lembra que a gente quer o valor de
Ah gente consegue mexer na expressão que temos e chegar nesse valor! Repara:
Chegamos! Percebe que o nosso índice só está com o nome diferente (está escrito em vez de ), mas fora isso está igualzinho. Então a gente pode dizer que:
Ufa! Conseguimos!
Resposta
a)
b)
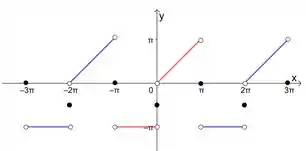
c)