Questão 4: Seja , para e para . Denotamos por a soma da série de senos da função . Quais são os valores de ?
Passo 1
Pow acho interessante aqui começarmos por um esboço da , neh?
Sabemos que possui esse perfil aqui para :
Então estamos falando de uma parábola:
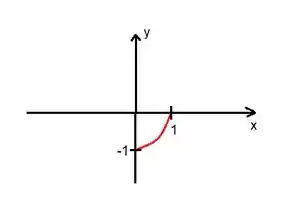
Como para , isso significa que o e o . O que estou tentando te dizer é que esse pedacinho de parábola vai se repetir no intervalo de a :
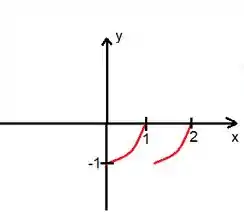
Passo 2
Agora, toda vez que tivermos falando de série de Fourier, temos que necessariamente ter uma função periódica infinita. No nosso caso, a função não é periódica infinita . Mas a gente pode construir uma extensão periódica não é verdade?
Podemos construir uma extensão tanto em cossenos, ou também conhecida como par, como podemos construir uma em senos, conhecida como ímpar. Pelo enunciado, é essa última aí que queremos!
A extensão ímpar tem que ser refletida duas vezes, uma pro lado e depois pra cima:
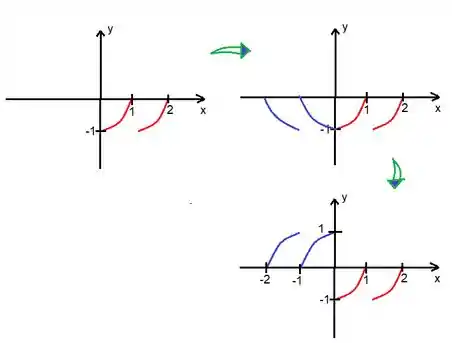
Agora é só colocar esse padrão de a se repetir... Em termos matemáticos, dizemos que, para o intervalo que vai de :
Saca? Pois e .
Passo 3
Sabemos ser a soma de Fourier, , igual ao valor da função onde é contínua e...
Para quando a função é descontínua! Onde é o valor da função pela esquerda, e o valor pela direita.
No caso de , trata-se de um ponto de descontinuidade:
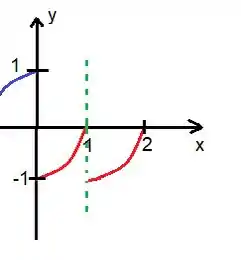
Veja que pela esquerda é , enquanto que pela direita, ele é , logo:
No caso do :
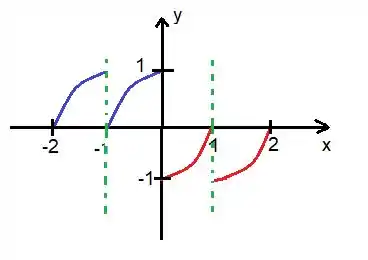
O é , já a função pela esquerda é :
Agora, para o , como estamos falando de um ponto na definição contínua da , a soma de Fourier é igual a função no ponto:
E quem é a função no ponto? Como se trata de um intervalo de , como discutido no passo anterior:
Logo...
Resposta
Alternativa