Para todas as funções cuja séries de Fourier você calculou nos exercícios e e , e .
Em quais pontos do intervalo vale que ?
Passo 1
Eaew, belezinha?
Este problema pede para analisarmos as séries de Fourier calculadas em outros exercícios, e analisarmos porquê as funções respeitam o teorema de convergência das séries de Fourier, nesta alternativa em particular, precisamos indicar em que intervalo de , cada uma delas pode ser identificada como , as funções são as seguintes
, estendida de forma -periódica;
e caso contrário.
e caso contrário.
e caso contrário.
Note que as questões acima não batem com as indicadas no enunciado, mas é porque aparentemente a professora cometeu um erro de digitação, a questão na verdade é uma EDP para ser resolvida e não tem alternativas. O teorema de convergência de Fourier é o seguinte
“Seja uma função periódica seccionalmente contínua em , então a série de Fourier converge para todo real e converge da seguinte forma
se é contínua em
se é descontínua em ”
Vamos usar isso para analisar as nossas funções! Vem comigo!
Passo 2
Primeiro, vamos lembrar o que é uma função seccionalmente contínua. Essas funções são aquelas que a descontinuidade é apenas na forma de pequenos saltos, a melhor maneira de explicar é visualizando, são funções do tipo
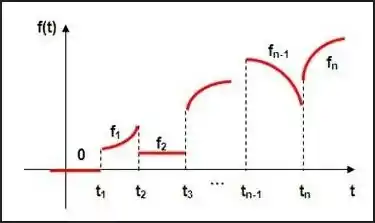
As três funções da questão são contínuas em um intervalo , ou seja, em cada um destes intervalos o teorema de convergência de Fourier garante que
note que o intervalo indicado é aberto, pois, se fizermos a extensão periódica de e a convergência acima não é verdade para e . No entanto, a função é -periódica, e devido ao formato da função modular, temos que ela é contínua, e não simplesmente seccionalmente contínua, portanto, a convergência é garantida para todo valor de .
Vamos agora analisar as outras três funções! Saca só!
Passo 3
O enunciado da questão indica que as três funções estão definidas no intervalo , todas as três são seccionalmente contínuas, elas valem ou nos intervalos estabelecidos, então tem apenas descontinuidades do tipo salto! Aqui precisaremos analisar cada função individualmente. A função tem descontinuidades em e , portanto, nesses pontos a igualdade
não é válida. Mas, em todos os outros pontos no intervalo ela é, sendo assim para a primeira função, temos que
quando
note que todos os intervalos são abertos! Isso é bastante importante! Analogamente ao que fizemos acima, podemos escrever o intervalo para as outras duas funções como
quando
e
quando
A questão foi isso! Te vejo na próxima! Tchau Tchau!