Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema da Convergência de Fourier

Ver Teoria
Exercício 81234567910111213141516171819202122232425

Enunciado

Seja f : - 2,2 → R uma função ímpar, contínua, C 1 por partes com f 1 = 0 e cujo gráfico no intervalo [ 0,2 ] está esboçado a seguir

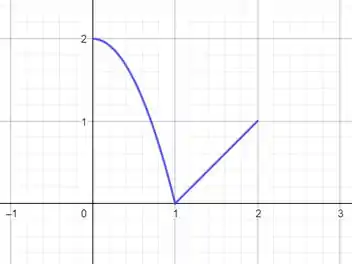
Sendo S ( x ) sua série de Fourier, analise as afirmações a seguir:

1   S x = S x + 2     p a r a   t o d o   x ∈ R

2   S n = 0   p a r a   t o d o   n ∈ Z

3   S x = f x   p a r a   t o d o   x ∈ ] 0,2 [

Podemos afirmar que:

( a ) Apenas ( 1 ) e ( 2 ) são verdadeiras

( b ) Apenas ( 1 ) e ( 3 ) são verdadeiras

( c ) Apenas ( 2 ) e ( 3 ) são verdadeiras

( d ) Todas as afirmações são verdadeiras

( e ) Nenhuma afirmação é verdadeira

Passo 1

Bom, começando pela primeira afirmação:

1   S x = S x + 2     p a r a   t o d o   x ∈ R

Cara, o período da série de Fourier dessa função vai ser o dobro do tamanho do intervalo em que ela está definida, isso porque dada uma função f definida no intervalo [ 0 , l ]

S x = S ( x + 2 l )

Então essa afirmativa é falsa, pois

S x = S x + 4

Passo 2

Agora analisando a segunda afirmação:

2   S n = 0   p a r a   t o d o   n ∈ Z

Essa afirmação é verdadeira.

Temos que:

S ± 2 = f 2 - + f - 2 + 2

Mas como f x é ímpar:

f 2 - = - f ( - 2 + )

S ± 2 = 0

E isso valerá para todo número par, porque se fizermos a extensão, veremos que os valores de S ( ± 2 ) são os mesmos de S ( ± 2 k ) .

Agora vamos pensar nos ímpares. Se fizermos a extensão, temos que:

S 2 k + 1 = S ( 1 )

Todos os números ímpares terão o mesmo valor da função que 1 . E dado que a função é contínua em ] 0,2 [ , temos que:

S 2 k + 1 = S 1 = f 1 = 0

Passo 3

Analisando a última informação:

3   S x = f x   p a r a   t o d o   x ∈ ] 0,2 [

Essa afirmativa é verdadeira, pois como f ( x ) é uma função contínua nesse intervalo, então S x = f ( x ) em ] 0,2 [ .

Resposta

c Apenas ( 2 ) e ( 3 ) são verdadeiras.

Exercícios de Livros Relacionados

Encontre a solução do problema de valor inicial y ' ' + ω 2 y = sen ⁡ n t , y 0 = 0 , y ' 0 = 0 Em que n é um inteiro positivo e ω 2 ≠ n 2 . O que acontece se ω 2 = n 2 ?
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = x + 1 , - 1 ≤ x0 , 1 - x , 0 ≤ x1 f x + 2 = f ( x ) (a) Encontre a série de Fourier da função dada.(b) Sej
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = 0 , - 1 ≤ x0 , x 2 , 0 ≤ x1 (a) Encontre a série de Fourier de função estendida.(b) Esboce o gráfico da fu
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = - 1 , - 1 ≤ x0 , 1 , 0 ≤ x1 (a) Encontre a série de Fourier de função estendida.(b) Esboce o gráfico da fu
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = 1 - x 2 , - 1 ≤ x1 (a) Encontre a série de Fourier de função estendida.(b) Esboce o gráfico da função para