Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema da Convergência de Fourier

Ver Teoria
Exercício 61234578910111213141516171819202122232425

Enunciado

Teste 3: Sejam f x uma função periódica de período 2 tal que f x = 4 - 4 x para 0 ≤ x ≤ 1 e f x = f x + 1 para - 1 < x < 0 , e S x a soma da sua série de Fourier. Então S 0 , S - 3 e S 3 / 2 valem, respectivamente:

  1. 2 ,   2 ,   2
  2. 2 ,   0 ,   - 2
  3. 4 ,   0 ,   2
  4. 4 ,   0 ,   - 2

Passo 1

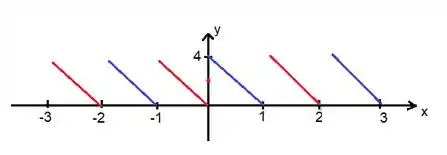
Pois bem, primeiro que tal desenharmos essa função durante um intervalo de - 3 a 3 ?

Bem, de 0 até 1 , a função é f x = 4 - 4 x :

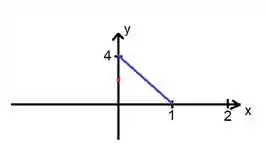
Enquanto que de - 1 a 0 ...

f x = f x + 1

Perceba que f - 1 = f 0 e f 0 = f 1 , isso significa que o f - 1 é o ponto maior da reta azul e o f 0 o ponto mais baixo gerando essa reta vermelha aqui:

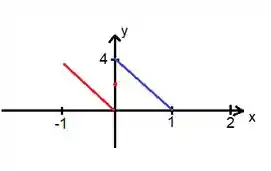
Perceba então que de - 1 a 1 , temos uma função de período 2 . Agora é só repetir o padrão...

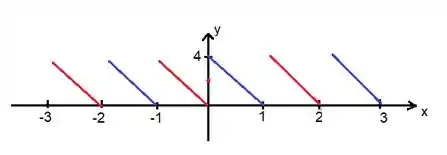
Passo 2

Ora, a soma de Fourier converge para a função, se estivermos em um trecho contínuo, ou para a media, se estivermos em um ponto de descontinuidade por pulos. Assim, a soma de Fourier em 0 é a média de f + 0 e f - 0 (função pela direita e pela esquerda):

f + 0 = 4 - 4 0 = 4

E

f - 0 = f 0 + 1 = 0

Logo...

S 0 = f + 0 + f - 0 2 = 4 + 0 2 = 2

Passo 3

Para S 3 2 , basta ver que 3 2 = 1,5 está na função contínua da retinha vermelha...

S 3 2 = f 3 2 = f 1 2 + 1 = f 1 2 =

4 - 4 1 2 = 2

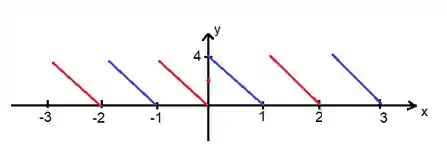
Passo 4

Por último S - 3 também se trata de um ponto de descontinuidade onde a função é 4 de um lado e 0 de outro como podemos ver no desenho...

Então

S - 3 = f - - 3 + f + - 3 2 = 2

Resposta

a )   2 ,   2 ,   2

Exercícios de Livros Relacionados

Encontre a solução do problema de valor inicial y ' ' + ω 2 y = sen ⁡ n t , y 0 = 0 , y ' 0 = 0 Em que n é um inteiro positivo e ω 2 ≠ n 2 . O que acontece se ω 2 = n 2 ?
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = x + 1 , - 1 ≤ x0 , 1 - x , 0 ≤ x1 f x + 2 = f ( x ) (a) Encontre a série de Fourier da função dada.(b) Sej
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = 0 , - 1 ≤ x0 , x 2 , 0 ≤ x1 (a) Encontre a série de Fourier de função estendida.(b) Esboce o gráfico da fu
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = - 1 , - 1 ≤ x0 , 1 , 0 ≤ x1 (a) Encontre a série de Fourier de função estendida.(b) Esboce o gráfico da fu
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = 1 - x 2 , - 1 ≤ x1 (a) Encontre a série de Fourier de função estendida.(b) Esboce o gráfico da função para