Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema da Convergência de Fourier

Ver Teoria
Exercício 11123456789101213141516171819202122232425

Enunciado

Teste 11: Seja f x = 1 2 - x para 0 , 1 2 e S x a soma da série de cossenos de f . No intervalo I = 7 2 , 9 2 , S x é dada por:

  1. S x = 1 2 - x
  2. S x = 1 2 - x + 8 2
  3. S x = 1 2 - x - 8 2
  4. S x = x - 8 2

Passo 1

Ora bolas, a soma da série de cosseno da função f nos define uma extensão par da função. Isso significa graficamente fazermos uma reflexão com relação ao eixo y :

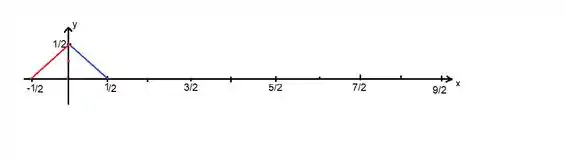
Matematicamente falando, a função de - 1 2 até 0 é definida apenas trocando-se o sinal de x na função de origem:

f x = 1 2 - x   →

g x = 1 2 + x

Ou seja, a extensão par de f que vamos chamar de f ~ é:

f ~ x = 1 2 - x ,     0 ≤ x ≤ 1 2   1 2 + x ,       - 1 2 ≤ x < 0

Agora é só dizer que f ~ x = f ~ x + 1 , pois isso significa que temos uma repetição periódica de período 1 . Em outras palavras, basta graficamente repetir esse padrão...

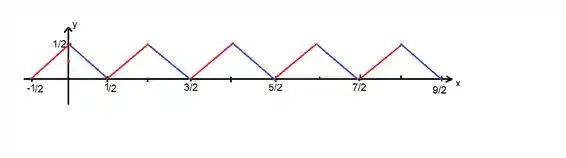
Pelo desenho e pela fórmula podemos ver que...

f ~ x = f ~ x + 1 = f ~ x + 2 = f ~ x + 3 = f ~ x + 4

Ou ainda somando 1 / 2 ao x de todas essas igualdades...

f ~ x + 1 2 = f ~ x + 3 2 = f ~ x + 3 2 = f ~ x + 5 2 = f ~ x + 7 2 = f ~ x + 9 2

Ou seja:

f ~ x + 7 2 = f ~ x + 1 2   →

f 7 2 = f 1 2 = 0

Ou ainda:

f ~ x + 9 2 = f ~ x + 1 2

f ~ 9 2 = f ~ 1 2 = 0

Agora quanto ao ponto do meio 4 ...

f ~ x + 4 = f ~ x     →

f ~ 4 = f ~ 0 = 1 2  

O que acabamos de fazer fora encontrar matematicamente os extremos desse 5 º triângulo aqui:

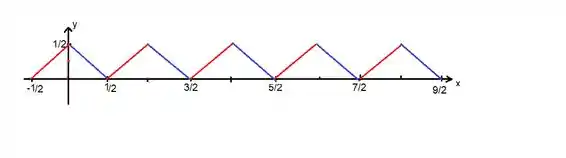
Isso tudo significa que de 7 / 2 a 4 a gente tem um deslocamento da reta vermelha de 8 / 2 para frente:

1 2 + x - 8 2 ,     7 2 < x < 4

Já para x de 4 a 9 / 2 , temos um deslocamento da reta azul em 8 2 também:

1 2 - x - 8 2 ,     4 ≤ x ≤ 9 2

Ótimo, então podemos concluir que:

S x = 1 2 + x - 8 2 ,     7 2 < x < 4   1 2 - x - 8 2 ,     4 ≤ x ≤ 9 2

E o que significa esse módulo aqui que aparece com frequência nas respostas?

x - 8 2

Pow! Ele é menos o termo de dentro se x < 8 / 2 e ele é mais se x ≥ 8 / 2 , certo? Definição de módulo isso aí:

x - 8 2 = - x - 8 2 ,         p a r a     x < 8 2

x - 8 2 = + x - 8 2 ,         p a r a     x ≥ 8 2

Então outra forma de expressar o S é:

S x = 1 2 - - x - 8 2 ,     7 2 < x < 4   1 2 - + x - 8 2 ,     4 ≤ x ≤ 9 2           →

Juntando essas duas coisas

S x = 1 2 - x - 8 2 ,     p a r a 7 2 ≤ x ≤ 9 2

Resposta

C )   S x = 1 2 - x - 8 2

Exercícios de Livros Relacionados

Encontre a solução do problema de valor inicial y ' ' + ω 2 y = sen ⁡ n t , y 0 = 0 , y ' 0 = 0 Em que n é um inteiro positivo e ω 2 ≠ n 2 . O que acontece se ω 2 = n 2 ?
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = x + 1 , - 1 ≤ x0 , 1 - x , 0 ≤ x1 f x + 2 = f ( x ) (a) Encontre a série de Fourier da função dada.(b) Sej
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = 0 , - 1 ≤ x0 , x 2 , 0 ≤ x1 (a) Encontre a série de Fourier de função estendida.(b) Esboce o gráfico da fu
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = - 1 , - 1 ≤ x0 , 1 , 0 ≤ x1 (a) Encontre a série de Fourier de função estendida.(b) Esboce o gráfico da fu
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original. f x = 1 - x 2 , - 1 ≤ x1 (a) Encontre a série de Fourier de função estendida.(b) Esboce o gráfico da função para