Para todas as funções cuja séries de Fourier você calculou nos exercícios e e , e .
Esboce o gráfico de no intervalo
Passo 1
Eaew, belezinha?
Este problema pede para analisarmos as séries de Fourier calculadas em outros exercícios, e analisarmos porquê as funções respeitam o teorema de convergência das séries de Fourier, nesta alternativa em particular, precisamos esboçar os gráficos de , a série de Fourier, as funções são as seguintes
, estendida de forma -periódica;
e caso contrário.
e caso contrário.
e caso contrário.
Note que as questões acima não batem com as indicadas no enunciado, mas é porque aparentemente a professora cometeu um erro de digitação, a questão na verdade é uma EDP para ser resolvida e não tem alternativas. O esboço do gráfico destas séries segue um padrão bastante simples de replicar, vamos partir dos gráficos das funções estendidas para o intervalo e então esboçar o resultado tendo em vista o teorema de convergência das séries de Fourier! Bora lá!
Passo 2
O gráfico da função estendida para o intervalo é tal que
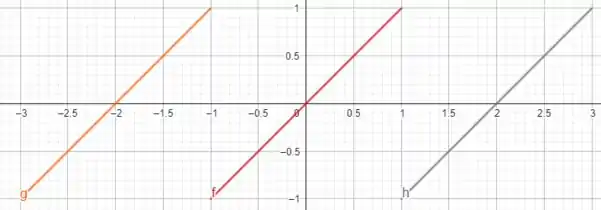
note que usei simplesmente para realizar o plot, você poderia escolher qualquer valor! Mas esse é o plot de , como seria o esboço de ? O formato desta série é tal que
esta série tem um padrão oscilatório devido às funções trigonométricas, e além disso, ela converge para a função nos pontos em que é contínua e converge para
nas descontinuidades! Ou seja, ao se aproximar dos pontos em que temos o salto, o valor de se afasta um pouco da função, mas mantendo um formato oscilatório! Esse padrão é tal que
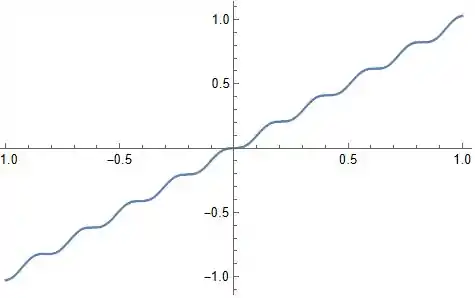
esse é o padrão no intervalo , note que para a extensão, isso deve se repetir em cada uma das seções da função e passar pelo valor médio nas desigualdades, ou seja, obtemos algo como
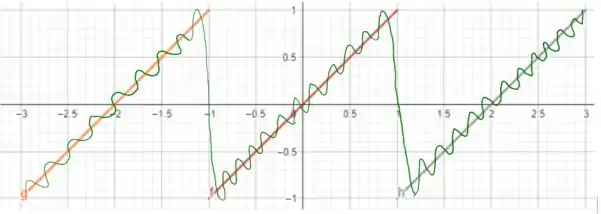
A ideia é a mesma para todas as outras! Vou apenas colocar elas nos próximo passo! Saca só!
Passo 3
Para a função temos
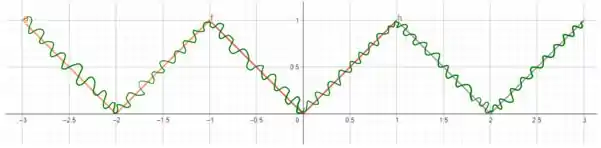
Para a função
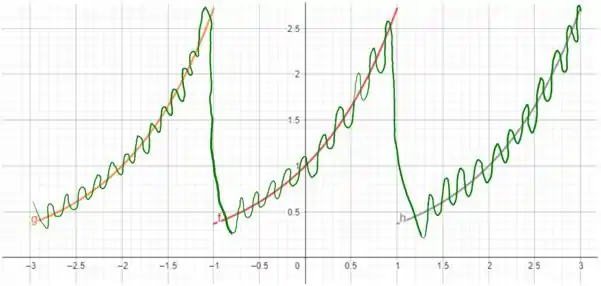
Para a função

Para a função

Para a função

Uff… A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!