Teste 13: seja uma função ímpar, por partes, com e cujo gráfico no intervalo está esboçado a seguir:
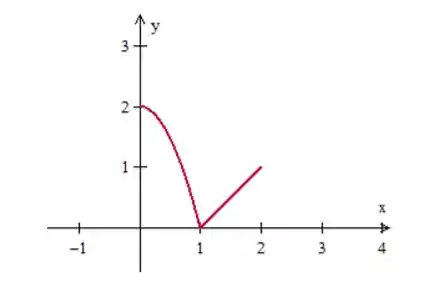
Sendo a soma da sua série de Fourier, analise as afirmações a seguir:
- para todo
- para todo
- para todo
- para todo
Podemos afirmar que:
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
Passo 1
Vamos analisar cada um e dizer se é verdadeiro ou não, ok? Antes porém, só perceba que a série de Fourier precisa de uma função periódica, então periodizando a nossa função de uma forma que ela seja uma função impar como no enunciado...
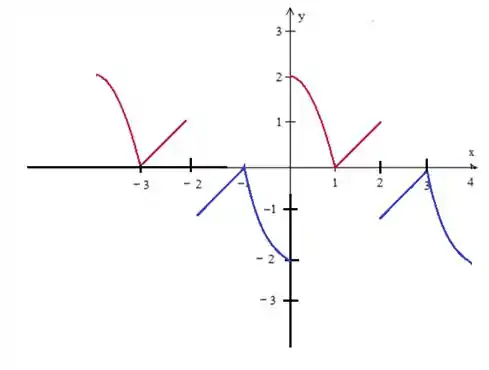
Passo 2
Primeiro a afirmação .
Ora, toda vez que temos um pertencente aos inteiros em temos de um número par, por exemplo:
Quem é ?
SIM! Como a função é descontínua nesse ponto, será a média dos valores da função nesse ponto. Como temos pela esquerda e pela direta , a soma de Fourier então é...
Para os também será , pois é já o de pela direita é menos :
Como a função é periódica, em todo par, de fato, teremos . Então a afirmação é falsa.
Passo 3
Ora, não! Sabe o porquê? Veja aqui então:
É de fato a caracterização de uma função periódica de período . Só tem um probleminha: A nossa função além de ser ímpar ela é de período :
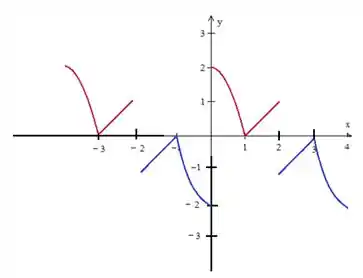
Por isso que no desenho ela repete o padrão a cada valores de , então o correto seria dizer que:
Ou ainda, como ela é uma extensão ímpar (o de baixo é o inverso do de cima):
Passo 4
Essa terceira é verdadeira!
já que estamos falando de um intervalo aberto onde a função é totalmente contínua pelo teorema de Fourier essas funções devem ser iguais.
Passo 5
Por último, vamos analisar a :
para todo .
Ora, sabemos que com relação aos números pares isso é verdade, pois analisamos lá no passo 2. Como os números inteiros podem ser divididos em números pares e ímpares:
Resta saber os resultados dos ímpares:
Veja na figura que em todos os termos ímpares como , , etc. a função é . Como quando a função é contínua, então de fato os termos ímpares são . Portanto a alternativa é verdadeira!
Resposta
D - Apenas e são verdadeiras.