UFMG, Sem campus, Equações Diferenciais B, Listas de EDB - Profª Aniura Milanés - Exercícios de EDB - 2021, Questão 20a
Para todas as funções cuja séries de Fourier você calculou nos exercícios e e , e .
Explique por que estas funções satisfazem as hipóteses do teorema de convergência das séries de Fourier estudado nesta semana.
Passo 1
Eaew, belezinha?
Este problema pede para analisarmos as séries de Fourier calculadas em outros exercícios, e analisarmos porquê as funções respeitam o teorema de convergência das séries de Fourier, as funções são as seguintes
, estendida de forma -periódica;
e caso contrário.
e caso contrário.
e caso contrário.
Note que as questões acima não batem com as indicadas no enunciado, mas é porque aparentemente a professora cometeu um erro de digitação, a questão na verdade é uma EDP para ser resolvida e não tem alternativas. O teorema de convergência de Fourier é o seguinte
“Seja uma função periódica seccionalmente contínua em , então a série de Fourier converge para todo real e converge da seguinte forma
se é contínua em
se é descontínua em ”
Vamos usar isso para analisar as nossas funções! Vem comigo!
Passo 2
Primeiro, vamos lembrar o que é uma função seccionalmente contínua. Essas funções são aquelas que a descontinuidade é apenas na forma de pequenos saltos, a melhor maneira de explicar é visualizando, são funções do tipo
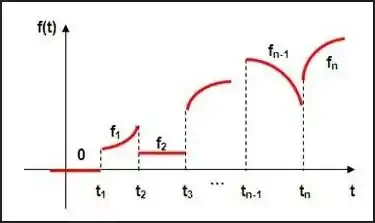
nas funções do exercício , temos que e são funções contínuas para todo , portanto, elas são seccionalmente contínuas. Mas, elas não são periódicas. Parece então que o teorema falha não é? Na verdade não! Essas duas funções estão definidas apenas em um intervalo , portanto, ela foi construída de forma que é uma função de período , mas ela se repete apenas uma vez! Uma análise parecida vale para a função , mas essa ainda é mais direta, pois nos é afirmado que ela é estendida de forma -periódica, ou seja, é como se a função se repetisse a cada .
Maravilha! As três respeitam o teorema de convergência de Fourier! Vamos analisar agora as funções do exercício . Vem comigo!
Passo 3
O enunciado da questão indica que as três funções estão definidas no intervalo , todas as três são seccionalmente contínuas, elas valem ou nos intervalos estabelecidos, então tem apenas descontinuidades do tipo salto! Novamente, elas não são por si só periódicas, mas por estarem definidas apenas em um intervalo limitado do tipo garante que a série de Fourier converge para esse intervalo, já que estamos trabalhando em um período .
No entanto, para que elas convirjam em todo , seria necessário fazer uma extensão -periódica. A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!