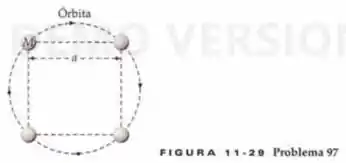
Quatro planetas idênticos formam um quadrado, como mostrado na Figura 11-29. Se a massa de cada planeta é e o lado do quadrado tem comprimento , qual deve ser a rapidez de cada planeta, se eles devem permanecer em órbita em torno de seu centro comum, sob a influência de suas atrações mútuas?
Passo 1
Como o arranjo é simétrico, cada planeta vai apresentar a mesma força centrípeta, que aponta para o centro do quadrado. Dessa forma, vamos pegar um planeta e calcular a força centrípeta agindo sobre ele.
Passo 2
Vamos calcular então a força centrípeta resultante no planeta indicado:
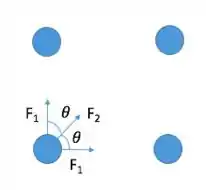
A força centrípeta aponta para o centro do quadrado, logo:
Substituindo os valores:
Passo 3
Sabemos que a força centrípeta tem a seguinte fórmula:
onde , que é o raio da órbita.
Logo, igualando as duas expressões que achamaos para a força centrípeta, teremos: