Satélites são ditos geoestacionários (ou geossincrônicos) quando executam uma órbita circular equatorial em torno da Terra com período de 24h. Isto é, o período do satélite é igual ao período de rotação da Terra. Para um observador no equador da Terra, o satélite comporta-se como se estivesse estacionário num local fixo no céu. Qual afirmação é verdadeira para um satélite em tal órbita?
(A) Não há força gravitacional agindo no satélite.
(B) O satélite não está sujeito a nenhuma aceleração.
(C) Só existe um raio que permite uma órbita geoestacionária.
(D) Existe uma força tangencial que ajuda o satélite a acompanhar a rotação da Terra.
(E) A força gravitacional é equilibrada por uma força que aponta para longe do centro da Terra.
Passo 1
Quando o satélite está em órbita, existe apenas uma força atuando sobre ele, a força gravitacional :
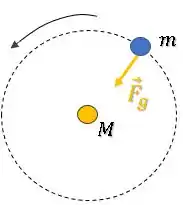
Essa força gravitacional que sempre aponta para o centro da trajetória gera uma aceleração que também aponta para o centro.
Além disso, se o satélite está em órbita, isso significa que a força gravitacional é igual à força centrípeta necessária para mantê-lo nessa trajetória circular.
Igualando as duas expressões, temos:
Então, a velocidade orbital depende da distância que o satélite está da Terra.
Podemos ainda relacionar com o período de uma volta completa:
Então, o período é:
Ou seja o período de revolução do satélite também depende da distância do satélite ao centro da Terra.
Portanto, só existe um raio que faz com que o período seja de 24h.
Então ficamos com a letra (C).
Resposta
Letra (C)