Escreva na forma sem calcular e .
Passo 1
Vamos lá, sabemos que a aceleração pode ser escrita na forma
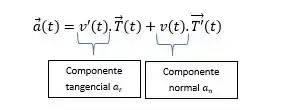
Onde .
Passo 2
Assim, pra descobrir as componentes normal e tangencial, precisamos calcular :
Então
Passo 3
Da fórmula, sabemos que
Então:
Resposta
Exercícios de Livros Relacionados
Determinar os vetores velocidade e aceleração para qualquer instante t . Determinar, ainda, o modulo desses vetores no instante dado.c) r → t = cosh ti → + 3 s e n h tj →; t = 0
Determinar os vetores velocidade e aceleração para qualquer instante t . Determinar, ainda, o modulo desses vetores no instante dado. r → t = 2 cos t i → + 5 s e n tj → + 3 k →; t = π / 4
Uma partícula se move no espaço com vetor posição r → t . Determinar a velocidade e a aceleração da partícula em um instante qualquer. Esboçar a trajetória da partícula e os vetores velocidade e acele
Determinar os vetores velocidade e aceleração para qualquer instante t . Determinar, ainda, o modulo desses vetores no instante dado.b) r → t = e ti → + e - 2 tj →; t = ln 2
Uma partícula se move no espaço com vetor posição r → t . Determinar a velocidade e a aceleração da partícula em um instante qualquer. Esboçar a trajetória da partícula e os vetores velocidade e acele