Livro James Stewart, Volume 2, 7ª Edição, Capítulo 13, Seção 4, Exercício 4
(Capítulo 13.4 – Exercício 4) Determine a velocidade, a aceleração e a velocidade escalar da partícula cuja função posição é dada. Esboce a trajetória da partícula e desenhe os vetores velocidade e aceleração para os valores de t especificados.
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
O objetivo dessa questão aqui, é determinar a velocidade, a aceleração e a velocidade escalar da partícula, a partir de uma função posição que nos foi dada. Mas como faremos isso?
Basta a gente lembrar da literatura, que a velocidade de uma partícula pode ser encontrada a partir da derivação de sua função posição!
Já a aceleração, será a derivada da derivada da função posição, ou seja, a derivada segunda da posição ou a derivada da velocidade.
E por fim, a velocidade escalar é dada pelo cálculo da norma do vetor aceleração.
Passo 2
Então, vamos começar encontrando a velocidade. O enunciado deu pra gente que a posição da partícula é a seguinte:
Derivando a função acima, vamos ter:
Além disso, o enunciado nos forneceu o valor de , que é igual a 1. Então já podemos substitui-lo na velocidade acima:
Pronto! A velocidade nós já temos. Bora calcular a aceleração então!
Passo 3
Como foi falado no passo 1, a aceleração se dá pela derivada segunda da função posição da partícula, ou seja:
E em :
Passo 4
Por fim, pra gente encontrar a velocidade escalar, precisamos da norma do vetor aceleração. Pra isso, vamos assumir um sistema de coordenada ortogonal e tirar a raiz quadrada da soma dos quadrados de cada uma dessas coordenadas (que é encontrada pela velocidade).
Esse sistema de coordenadas foi encontrado no passo 2:
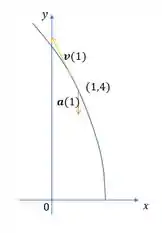
Prontinho! Agora só falta esboçarmos a trajetória da partícula e desenhar os vetores velocidade e aceleração para os valores de .
Então, vamos ter que:
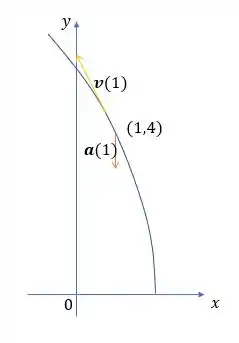
Pra essa questão é isso, pessoal!! Bora resolver mais uma??
Resposta
