Calcular a massa do sólido limitado por , e , de densidade .
Passo 1
O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por . Nós sabemos que:
Onde é o diferencial de massa e o de volume. Integrando ambos os lados na região em que o sólido está contido, temos que:
Passo 2
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos uma esfera de raio , dada por e as superfícies e . Depois nos preocupamos com os sinais.
Para trabalhar com módulos, temos que pensar da seguinte forma: de o número é positivo ou nulo, então , se for negativo, .
Assim, podemos separar cada uma dessas equações com módulos em duas:
Ok? Temos vários planos então, não é? Vamos desenhar isso tudo.
Como todos os planos são perpendiculares ao plano (só possuem essas duas variáveis na equação), vamos desenhar a região vista de cima para ficar mais fácil. Ou seja, esses plano viram retas.
Pensando no primeiro par de planos, temos , como o coeficiente de é negativo, sabemos que a inclinação da reta é para a esquerda. Quando , , logo, a reta corta o eixo em Para fazer a outra reta , podemos só espelhar essa que fizemos em relação ao eixo , pois elas são simétricas, tem o mesmo formato, porém sinal contrário de . Ou você pode seguir o mesmo raciocínio que fizemos para a primeira reta. Assim temos esse par de retas verdes que está aí embaixo.
Para o outro par de retas, basta seguir o mesmo pensamento. Por exemplo tem coeficiente de positivo, logo, a reta é inclinada para a direita, cortando o eixo em . Espelhando essa reta, temos esse par de retas azuis, na figura abaixo.
Como podemos ver, a esfera de raio , vista de cima, é esse círculo de raio em vermelho.
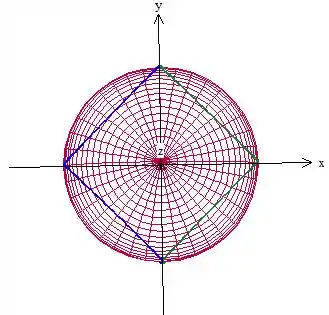
Agora que deu para a gente entender o que está acontecendo, vamos desenhar no :
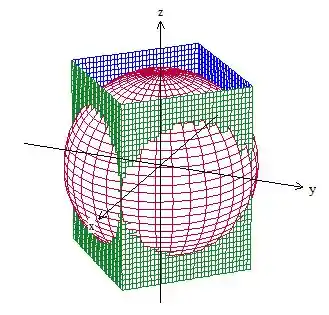
É isso aqui o que temos. Agora chegou a hora de vermos os sinais. Temos , logo, queremos o que está dentro da esfera. Para os planos, temos e . Como temos “módulo menor ou igual a alguma coisa”, queremos tudo o que tem valor absoluto de menor ou igual ao do plano, portanto, dentro dessa região limitada pelos quadro planos. Sacou?
Então, nossa região é o o que está dentro da esfera e dentro da região limitada pelos planos, portanto, a esfera sem essas calotas que o planos cortaram.
Passo 3
Tá, antes de continuarmos, vamos fazer uma observação importante. Olha de novo a região vista de cima:
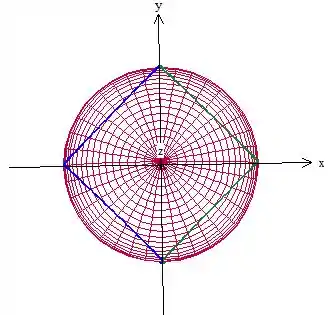
Nossa região é o que está dentro do quadrado. Reparou que temos muita simetria aí, né? Podemos dividir essa região em 4 partes e calcular apenas a massa de uma dessas partes. Depois, é claro, mutiplicamos por 4 o resultado.
Mas podemos mesmo fazer isso? A função densidade varia. Podemos porque em tanto o como o estão elevados ao quadrado, assim:
Ou seja, em todos os quadrantes a distribuição da função densidade é a mesma.
Pera, reparou que independe de ? Não temos na sua expressão. Isso significa que podemos dividir mais ainda a região, nos diedros. É como se tivéssemos 4 partes de massa igual para o positivo e para o negativo.
Então, chamando de a massa da parte do sólido que está no octante com , e , temos:
Ou seja, vamos calcular a massa desse pedaço aqui:
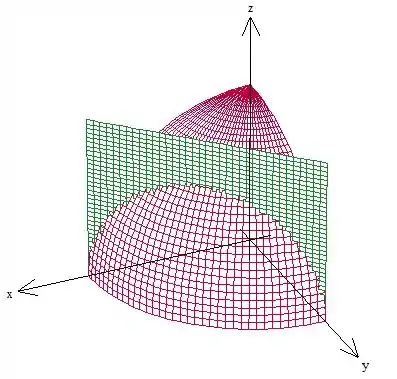
Passo 4
Vamos agora escrever matematicamente essa região. Como podemos ver pela figura, varia entre e a superfície da esfera, logo, . No plano , temos como domínio uma região que, como podemos ver, é um triângulo. Depos nois preocupamos com , ok?
Passo 5
Agora vamos escrever essa região .
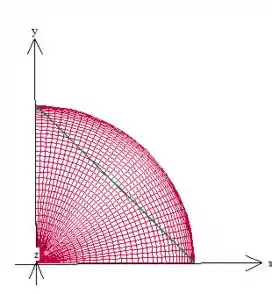
Escrevendo como região do tipo I, temos entre e a reta , ou seja e (como já vimos, as retas cortam os eixos em e ). Isso nos dá:
Passo 6
Agora vamos resolver isso aí