Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Centroide de Sólidos

Ver Teoria
Exercício 2134567891011121314151617181920

Enunciado

Use coordenadas cilíndricas para encontrar o centroide do sólido limitado acima pela esfera

x 2 + y 2 + z 2 = 2

E abaixo pelo paraboloide

z = x 2 + y 2

Passo 1

Como vamos usar as coordenadas cilíndricas para resolver nosso problema! As coordenadas cilíndricas são r ,   θ e z .

x = r ⋅ cos ⁡ θ y = r ⋅ s e n   θ z = z

Se quiser visualizar melhor o problema, o esboço é esse aqui

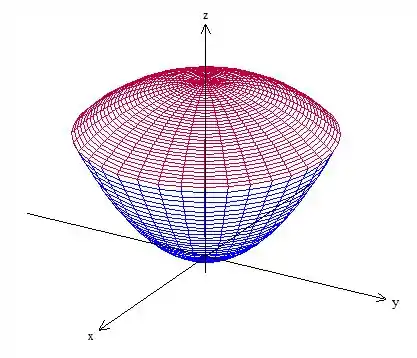
Passo 2

Agora devemos encontrar os limites das variáveis, para isso vamos determinar os limites das variáveis e para isso precisamos da intercessão entre a esfera e o paraboloide:

Substituindo a equação do paraboloide na equação da esfera temos,

z + z 2 = 2 → z 2 + z - 2 = 0

Esta equação tem raízes z = 1 e z =   - 2

Como z = x 2 + y 2 , ou seja, a soma de dois quadrados, tem que ser positivo pois estamos trabalhando com números reais. Logo, z = 1

Passo 3

Assim, temos que, ao usar as coordenadas cilíndricas:

Para a variável z , seus limite superior é a esfera, logo

z ≤ 2 - x 2 - y 2 → z ≤ 2 - r 2

Seu limite inferior é dado pelo paraboloide, logo

z ≥ x 2 + y 2 →     z ≥ r 2

Assim,

r 2 ≤ z ≤ 2 - r 2

Para a variável r ,   ela vai variar ate no máximo o valor da intercessão entre a esfera e o paraboloide, lembra que encontramos esse valor lá em cima? A interseção das superfícies é dada em

x 2 + y 2 = 1

Com isso,

0 ≤ r ≤ 1

Por último,

0 ≤ θ ≤ 2 π

Passo 4

Vamos calcular o centróide agora!! Como o sólido é simétrico em relação ao eixo z , temos que

x c = y c = 0

Para calcular y c   vamos usar a fórmula:

z c = ∭ W z d V ∭ W d V = 1 V ∭ W z d V

Calculando o volume,

V = ∫ 0 2 π ∫ 0 1 ∫ r 2 2 - r 2 r   d z d r d θ   = ∫ 0 2 π ∫ 0 1 r ⋅ 2 - r 2 - r 2 d r d θ    

V =   ∫ 0 2 π ∫ 0 1 r 2 - r 2 - r 3 d r d θ   = 2 π ⋅ 2 3 ⋅ - 1 2 ⋅ 2 - r 2 3 2 - r 4 4 0 1

V = 2 π ⋅ - 1 3 - 1 4 + 8 3 = 8 2 - 7 ⋅ π 6

Vamos calcular a integral

∭ W z d V =   ∫ 0 2 π ∫ 0 1 ∫ r 2 2 - r 2 z r   d z d r d θ   =   ∫ 0 2 π ∫ 0 1 r ⋅ z 2 2 r 2 2 - r 2 d r d θ  

∭ W z d V = ∫ 0 2 π ∫ 0 1 r ⋅ 1 2 ( 2 - r 2 - r 4 ) d r d θ   = 2 π ⋅ 1 2 r 2 - r 4 4 - r 6 6 0 1 = 7 π 12  

Assim,

z c = 6 8 2 - 7 π 7 π 12 =   7 16 2 - 14

O centóide será,

x c ,   y c ,   z c =   0 ,   0 , 7 16 2 - 14

Resposta

O centroide será

x c ,   y c ,   z c = 0 ,   0 , 7 16 2 - 14  

Exercícios de Livros Relacionados

Determine a massa e o centro de massa do sólido dado E com função densidade dada ρ . E é o tetraedro limitado pelos planos x = 0 ,y = 0 ,z = 0 ,x + y + z = 1 ρ x , y , z = y
Utilize coordenadas esféricas.Determine o centroide do sólido do exercício 25.
Determine o centro de massa de uma semi-esfera, cuja densidade no ponto P é proporcional à distância de P ao centro.
Estabeleça, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inercia em relação ao eixo z.39. O sólido do exercício 19; ρ x , y , z = x 2 + y 2
Estabeleça, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inercia em relação ao eixo z.40. O hemisfério x 2 + y 2 + z 2 ≤ 1 , z ≥ 0 ;ρ x , y , z =