Calcule massa do sólido limitado por e , de densidade .
Passo 1
O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por . Nós sabemos que:
Onde é o diferencial de massa e o de volume. Integrando ambos os lados na região em que o sólido está contido, temos que:
Passo 2
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos uma esfera , de raio e a superfície , que é um cone com centro deslocado no eixo , no caso, para o ponto . Portanto, isso aqui:
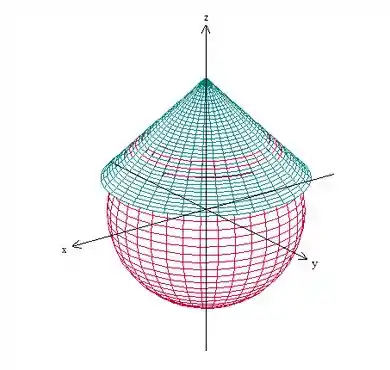
E a região do problema é aquela que está fora da esfera, por causa do sinal em e abaixo do cone, pelo sinal em Show?
Obs: temos só a folha debaixo do cone porque a equação e nos dá a condição , logo, . Isso porque a raiz tem que ser não nula.
Passo 3
Como a região é limitada por uma esfera e um cone, vamos utilizar coordenadas esféricas:
Passo 4
Precisamos escrever matematicamente a região de integração.
Vamos começar pelo raio. Pela figura, sabemos que varia desde a superfície da esfera até o cone. Então, vamos fazer a mudança esférica na equação do cone:
Certo, então temos . Como temos uma volta completa em torno do eixo , . Agora vamos pensar no ângulo .
Sabemos que ele vai desde zero (o que ocorre no eixo até o ponto em que o cone corta a esfera. Vamos desenhar uma seção dessa região para entender melhor:
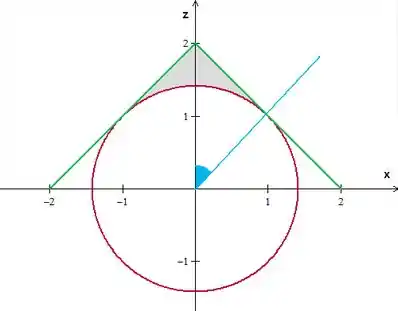
Em vermelho, temos uma seção da esfera no plano , em verde, temos uma seção do cone. Como falamos no início da questão, o máximo do cone é e ocorre quando seu raio é nulo. Dá para ver isso pela equação . Agora e esse ponto onde ele corta o eixo ? Esse é o raio do cone quando ele corta o plano , não é? Ou seja, quando . Fazendo na equação do cone, temos , logo, esse raio é , como está na figura. Ok, guarde essa informação.
Marcamos na figura, em cinza, a seção da região do problema, que está abaixo do cone e fora da esfera. Assim, podemos ver a variação do ângulo dessa região, que está marcada em azul.
Como já falamos, vai de zero até o ângulo onde as superfícies se cortam. Se você reparar, temos um triângulo retângulo isósceles com lados iguais de tamanho (tanto na esquerda como na direita). Sendo assim, essa reta azul, que é perpendicular à verde, é uma bissetriz do ângulo , formado entre os eixos e . Ou seja, esse ângulo marcado em azul é .
Assim, podemos dizer, para a nossa região, que .
Passo 5
Vamos agora (finalmente) fazer a substituição esférica na integral:
Passo 6
Agora vamos integrar em relação a :
Passo 7
Agora em relação a :
Passo 8
Vamos resolver a primeira integral, fazendo
Agora precisamos fazer a mesma substituição para a segunda integral:
E essa para a terceira:
Ok, agora vamos juntar isso tudo: