Seja uma região sólida no primeiro octante é limitada pelos planos coordenados e pelo plano . A densidade do sólido é . Encontre a massa do sólido e o centro de massa.
Passo 1
Primeiro vamos determinar os limites das variáveis, o solido é
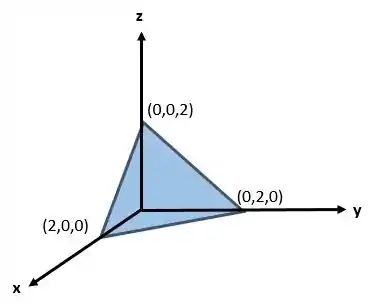
Então vamos começar fazendo,
Ao fixar um valor de , temos que vai variar da seguinte forma
Para entender isso, vamos olhar o plano , ele é limitado pelos eixos coordenados e pela reta Agora para um ponto determinado, a varável vai variar da seguinte forma
Agora que já temos os limites das variáveis no sólido, vamos ir para as integrais que usamos para calcular a massa e o centro de massa!
Passo 2
A massa do sólido é dada por,
Passo 3
Agora vamos calcular os momentos,
Como a equação é simétrica em e , ou seja, se trocarmos por e vice versa as equações não se alteram, temos que
Agora, por último temos
Passo 4
Já temos os momentos, agora vamos encontraro centro de massa:
Assim,