Questão 2:
Calcule a coordenada do centroide de .
Passo 1
Para encontrarmos o centro de massa, ou melhor, a coordenada dela como pede o problema, podemos simplesmente utilizar a relação:
Bem, então temos dois trabalhos a fazer aqui:
1º - Encontrar o Volume de .
2º - Em seguida determinar o valor dessa integral tripla em cima de .
Então vamos nessa?
Passo 2
Vamos começar com o Volume. Já sabemos que um determinado volume também pode ser calculado por uma integral tripla:
Mas repare que temos certo trabalho a fazer aqui, como primeiro descrever a região de integração em seguida calcular o volume.
Como , caso desenhamos em ...
Ou seja, uma esfera de raio , mas que está entre os planos e ...
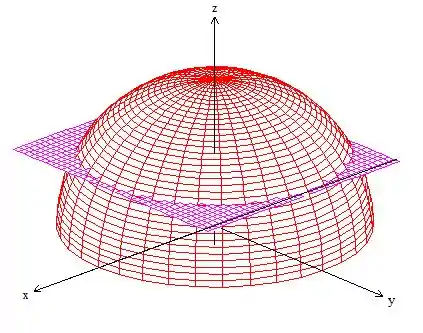
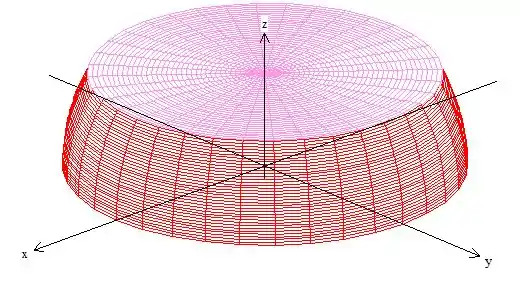
Repare que como estamos trabalhando com uma região que embora esteja dentro de uma esfera, descrever em coordenadas cilíndricas facilita mais, pois temos uma metade de esfera:
O Jacobiano dessas mudanças...
Além disso, a equação da circunferência ajuda muito:
Passo 3
Agora, não podemos sair da mudança enquanto não encontramos as variações de e ...
Para fazer isso, imaginemos esse tronco de esfera como se fosse um “monte” de círculos empilhados. Vamos descrever um círculo desses, como gira ao redor do eixo ...
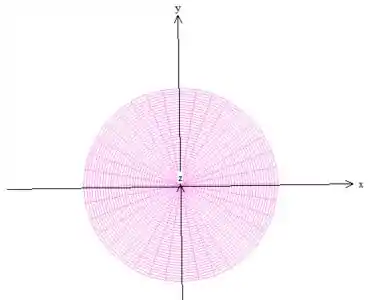
Para descrever o raio, repara que ele varia de até a borda da esfera de equação...
Substituindo as coordenadas cilíndricas...
Então o raio dentro desse círculo está variando de...
Descrevemos um círculo. Para descrever todo o volume , basta variar o de até :
Passo 4
Com o sólido descrito, podemos simplesmente voltar para a integral tripla do volume que queremos...
E substituir não esquecendo multiplicar pelo Jacobiano...
Integrando...
Passo 5
Ainda não terminamos, pois só determinamos o volume. Nos falta calcularmos aquela outra integral tripla antes de fazermos a fração...
Para resolver essa integral, com a descrição em coordenadas cilíndricas já resolvidas:
Podemos Já substituir...
Bora calcular a integral?
Passo 6
Substituindo os limites em ...
Agora substituindo os limites em ...
Passo 7
Então podemos concluir que...