Obtenha o centro de massa do sólido delimitado superiormente pela esfera e inferiormente pelo plano . Assuma que a densidade é contante.
Passo 1
Opa, vamos lá. Pra achar centro de massa é bem receitinha de bolo. Primeiro a gente tem de encontrar os e, lembra?
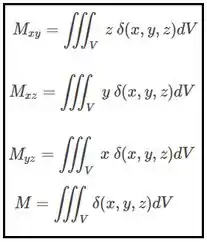
Não esquece que esse não é nada mais que a densidade, que na questão ele já nos disse que é .
Passo 2
Mas e esse sólido, como ele é?
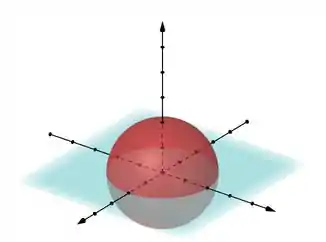
Eu quero que você perceba que eu não coloquei valores no gráfico, até pq a gente não sabe o tamanho do raio dessa esfera, só sabemos que vamos chamar de .
Passo 3
Então beleza, vamos juntar o que a gente tem até agora.
Observa comigo que esse M nada mais é do que o volume do sólido vezes esse , certo?
Qual o volume de esfera? Mas nesse caso nosso sólido é a metade da esfera. Então show, ficamos com .
Logo:
Passo 4
Bora agora partir pras coordenadas.

Como ficam as coisas então?
Passo 5
O próximo passos agora é resolver esse .
Como estamos lidando com uma esfera, vamos usar coordenadas esféricas, show?

Então vamo pras substituições.
Lembrando que o que eu coloquei ali é o Jacobiano que a gente não pode esquecer nunca!!
Estudando so intervalos de variação de e temos:
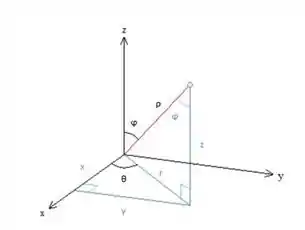
varia entre 0 e 2, uma vez que da uma volta completa, o vai de 0 a , que é o maior valor que o raio assume, e vai só de 0 a , já que se trata só da metade de cima de uma esfera.
Então ficamos com:
Fazendo
Fazendo as outras partes mais simples da integral
Então
Encontrando a coordenada de :
Passo 6
Faltam agora as coordenadas e . Mas essas são bem mais tranquilas! Por simetria o centro de massa tem de estar no eixo z! Ou seja