Calcule a massa do sólido que é parte da bola , acima do cone e abaixo do cone , com densidade .
Passo 1
O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por . Nós sabemos que:
Onde é o diferencial de massa e o de volume. Integrando ambos os lados na região em que o sólido está contido, temos que:
Passo 2
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos uma esfera de raio deslocada da origem em , ou seja, com centro em . Temos também dois cones: e . Para desenhar eles, você precisa notar que o primeiro tem uma abertura maior do que o segundo, pois, pensando em coordenadas cilíndricas, temos e (logo, para um mesmo , o do primeiro é menor).
Então, desenhando essas três superfícies, temos:
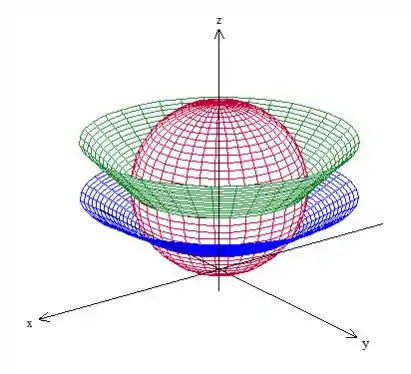
O problema pede o sólido que é parte da bola , está acima do cone (de abertura maior) e abaixo do cone (de abertura menor).
Cortando, temos isso aqui:
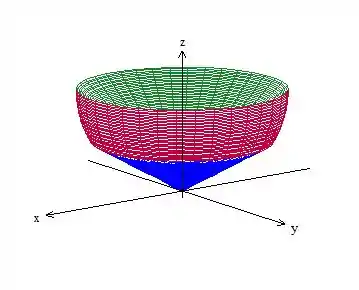
Show?
Passo 3
Como a região é limitada por uma esfera e um cone, vamos utilizar coordenadas esféricas:
Passo 4
Precisamos escrever matematicamente a região de integração.
O raio varia desde a origem, onde até a superfície da esfera. Como a esfera não está centrada na origem, precisamos fazer a mudança de coordenadas na sua equação para descobrir a expressão de :
Logo, temos .
Como temos uma volta completa em torno do eixo , temos .
E o ângulo , como vemos pela figura, varia desde a superfície de um cone até a do outro. Então vamos fazer a mudança esférica nos dois cones:
Logo,. Assim, temos a região:
Passo 5
Vamos agora (finalmente) fazer a substituição esférica na integral:
Passo 6
Agora vamos integrar em relação a :
Passo 7
Agora em relação a :
Passo 8
Agora, vamos fazer a substituição:
Levando isso para a integral, temos: