Calcule a massa do sólido dado por:

Tal que e com densidade .

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos uma esfera de raio centrada na origem e um cone com eixo de simetria em (que fica no lugar do eixo , que estamos acostumados a ver).

Para você saber qual o eixo de simetria do cone, basta você olhar para sua equação e encontrar o termo “diferente”, no caso, é o que tem sinal contrário a e a (fica do outro lado da equação). Em geral, temos o isolado, porque o eixo de simetria costuma ser esse.

Beleza, temos isso aqui:

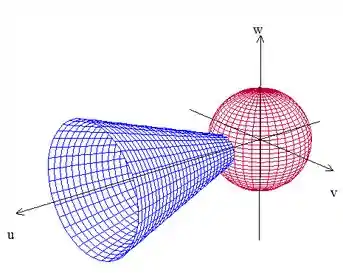
Nossa região é a que está dentro do cone e fora da esfera. Não podemos nos esquecer também que o problema diz que e que , portanto, temos isso aqui:

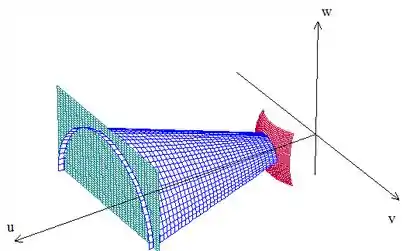
Beleza?

Como a região é limitada por uma esfera e um cone, vamos utilizar coordenadas esféricas:

Precisamos escrever matematicamente a região de integração.

Vamos começar pelo raio. Pela figura, sabemos que varia desde a superfície da esfera até a do plano . Temos, então, que escrever esse plano em coordenadas esféricas:

Nossa, isso aí vai ser péssimo para colocarmos na integral depois, não é? Sem condições. Ok, e agora?! Vamos pensar um pouco.

Senta, que agora a coisa ficou séria.

Se você reparar, as coordenadas esféricas são definidas com uma certa simetria em relação ao eixo (que costumamos chamar de ). Como assim? O ângulo é medido em torno desse eixo e o ângulo , a partir desse eixo. Por isso, quando temos um plano (paralelo a ) deslocado em , sua equação não fica tão complicada como quando está deslocado nos outros eixos. O mesmo vai acontecer para o cone.

Partindo dessa ideia, podemos, então, fazer uma mudança esférica diferente, atribuindo não ao eixo , mas ao eixo de simetria da região, no caso, o eixo . Teremos, então:

Bom, como a equação da esfera é , tanto faz a definição de , e , vamos continuar tendo . Agora, para as outras superfíces a coisa muda.

Vamos começar pelo plano:

Já melhorou, né? Sabemos, então, que .

Agora vamos analisar o ângulo . Lembra que ele era marcado em relação ao eixo ? (que chamamos de ). Como “trocamos” esse eixo com o , agora o vai ser marcado em relaçao a . Não tá entendendo nada? Respira. Calma que a gente te ajuda! Vamos ver essa região desse jeito aqui:

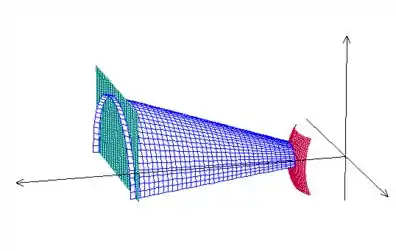
Esquece o nome dos eixos. Podemos ver que vai desde até a superfície do cone, não é? Então vamos fazer a mudançar polar na equação do cone:

Portanto, . Pela figura acima, vemos também que . Então, região será escrita como:

Vamos agora (finalmente) fazer a substituição esférica na integral:

Agora vamos integrar em relação a :

Agora em relação a :

Agora vamos integrar em relação a :