Com base no circuito abaixo, onde , considere as afirmações a seguir
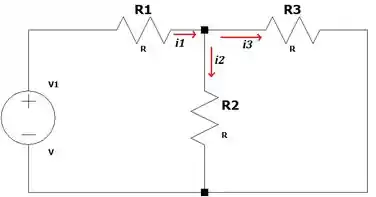
I)
II)
III) Se ,
Quais afirmações estão corretas?
a) Apenas I
b) Apenas II
c) Apenas III
d) I e II
e) II e III
Passo 1
Vamos analisar cada uma das afirmativas:
- Se ,
Bom, sabemos que a corrente será dividida nas corrente e , portanto:
Logo, é matematicamente impossível que a corrente seja maior que a corrente , logo essa é falsa.
Passo 2
Como dito no Passo 1, a corrente será:
Logo, isolando teremos:
E essa alternativa está correta.
Passo 3
Nesse caso, para a corrente ser zero é necessário que não haja corrente circulando no circuito, o que faria com que:
E assim, as correntes e são iguais, portanto, esta também está correta.
Portanto, a alternativa correta é a letra .
Resposta
e) II e III
Exercícios de Livros Relacionados
Enquanto você está reformando sua garagem, você precisa emendar temporariamente um fio de cobre de 80 m de comprimento e 1,00 mm de diâmetro com um fio de alumínio de 49 m de comprimento, que tem o me
A Figura 20.13 mostra um cone feito de material com resistividade ρ , com a ponta aparada por um plano paralelo à base. As duas faces circulares do corpo têm raios a e b , e forma metalizadas. Supondo
Mostre que a resistência elétrica de uma placa quadrada de espessura fixa, para correntes paralelas a uma de suas arestas, independe do tamanho da placa.
Seguindo o procedimento análogo ao do 20.6P, calcule a constante de tempo de um capacitor esférico preenchido por um dielétrico.
A Figura 20.12 mostra um capacitor cilíndrico preenchido por um material dielétrico de resistividade elétrica ρ e constante dielétrica κ . Uma bateria aplica uma voltagem V ao capacitor.a) Calcule a c