UFU, Sem Campus, Física 3, Provas Profa. Elisangela y Castro - P3 - 2022.1, Questão 2de
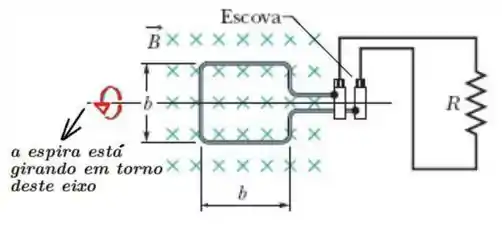
Uma espira quadrada de lado , é girada com uma frequência constante num campo magnético uniforme , entrando no plano da página, como mostra a figura abaixo. Considere a resistência total do sistema igual a . Calcule:
A corrente máxima induzida na espira.
Projete uma espira que produza uma com quando a frequência for em um campo magnético de , ou seja, calcule o lado (largura) da espira?
Passo 1
Fala aí pessoal, como é que vocês estão?
Bom, nessa questão temos uma espira que está girando em uma região de campo magnético. Essa rotação provoca a variação do fluxo magnético através da espira, e consequentemente (pela lei de Faraday), gera uma força eletromotriz induzida.
Usando a lei de Faraday:
Já calculamos no item anterior que a induzida vale:
E, usando a primeira lei de , encontramos também a corrente induzida:
Aqui, precisaremos avaliar a expressão da corrente induzida para encontrar o seu valor máximo.
Além disso, também precisaremos dimensionar uma espira para que a máxima seja de .
Vamo simbora que vai ficar bem claro 😊
Passo 2
Pra começar, no item , vamos determinar a corrente máxima induzida no circuito.
Já sabemos que:
Ou seja, a corrente induzida depende do tempo. Mas, a sua dependência com o tempo acontece no argumento da função seno. E, a função seno é limitada (varia sempre de a ).
Assim, vamos ter que a corrente induzida assume o seu valor máximo, quando o seno é máximo.
Logo:
Prontinho 😊
Passo 3
No item precisamos dimensionar a espira para que .
Mas podem ficar tranquilos pessoal, dimensionar significa apenas que iremos determinar as dimensões (comprimento e largura da espira).
Além do mais, como a espira é um quadrado nesse caso, precisamos apenas determinar o valor do parâmetro .
Para fazer isso, vamos encontrar uma expressão para a máxima induzida:
Novamente, a ideia é que o seno seja máximo. Assim, temos:
Como queremos que a seja no máximo , precisamos fazer:
O enunciado nos deu que e que , temos:
Logo:
Prontinho galera!
É isso! Matamos mais uma questão, muito obrigado pela atenção de vocês 😊