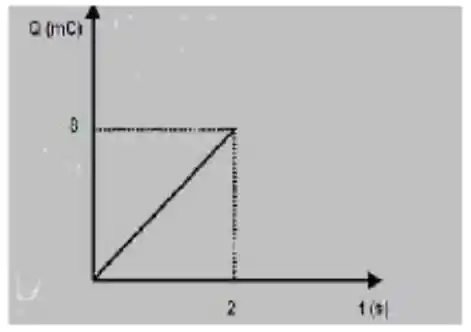
O gráfico a seguir mostra a variação da carga que atravessa um condutor em um determinado intervalo de tempo. Com base nos dados colhidos deste gráfico, podemos afirmar que a corrente elétrica que circula no condutor é igual a:
Passo 1
Não fica cabisbaixo só de ver um gráfico, gráficos dizem muitas coisas pra gente e são extremamente importantes, então agora bora matar essas questão.
Voce precisa se lembrar do que é a corrente elétrica. A corrente elétrica é a quantidade de carga que atravessa um condutor (um fio, por exemplo) em determinado intervalo de tempo, ou seja, podemos escrever a corrente elétrica como a taxa de variação da carga em um determinado tempo. Você lembra lá de calculo 1 o que é a taxa de variação?! A taxa de variação é a derivada né, então, escrevendo matematicamente,
Passo 2
Agora você deve ta pensando “Beleza, e no que isso me ajuda?” e eis a resposta, lembra que o enunciado nos deu um gráfico da carga em função do tempo?! Então vamos escrever uma função e depois derivar em relação ao tempo. E como fazer isso?! O gráfico é uma reta, e sabemos qual a equação de uma reta, que é do tipo
Então, para
Agora é só substituirmos os pontos mostrados no gráfico para encontrarmos nossa função, vamos lá
- Para o ponto , temos
- Para o ponto , temos
Então, descobrimos e , agora podemos escrever nossa função
Passo 3
Já temos a função, então o último passo é derivar essa função em relação ao tempo, derivando, vemos
Note que a unidade está em pois no gráfico a carga é dada em