A fonte de um circuito RLC fornece uma tensão de a uma frequência angular de . Um voltímetro ligado às extremidades do capacitor mede uma tensão de . Considere e . Qual é o modulo da impedância do circuito?
Passo 1
Para termos uma noção melhor de como resolver esse nosso problema, vamos desenhar o circuito do enunciado, pode ser?
Sabemos ser um circuito onde a gente não sabe muito sobre o resistor...
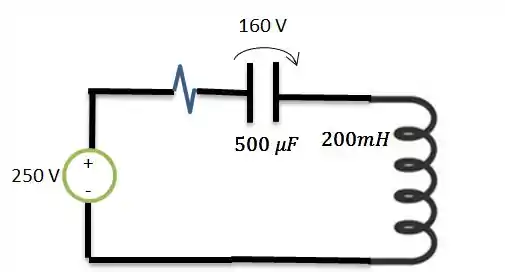
Uma forma de encontrar a impedância do sistema seria...
Mas infelizmente não temos a informação da resistência. Então, a melhor forma é pegando a tensão total da fonte e dividir pela corrente que o circuito demanda (Lei de Ohm):
Tá! Mas ainda precisamos saber quem é a corrente! Bora?
Passo 2
POW! Repare que temos a tensão em cima do capacitor () e temos a capacitância dele. Podemos aplicar a Lei de Ohm para esse elemento onde a gente vai obter...
Onde é obtido pela capacitância...
O problema nos disse que a frequência angular era de e que (ou )...
Então...
Passo 3
Com a corrente em mãos podemos encontrar então o módulo da impedância do sistema como vistos no passo 1:
Resposta
Letra B