A diferença de potencial sobre um capacitor de placas paralelas circulares de capacitância , onde o efeito de bordas foi desprezado, é dada por , com em segundos.
11 a) A corrente de deslocamento no capacitor vale:
- 1 mA
- 10 mA
- 100 mA
- 0,1 mA
- 0,01 mA
11 b) Sabendo a intensidade do campo elétrico nas placas do capacitor, a expressão para a intensidade do campo magnético dentro das placas do capacitor a uma distância do eixo de simetria é:
Passo 1
Temos um capacitor de placas paralelas circulares que está submetido à uma diferença de potencial que varia com o tempo. Como essa ddp depende diretamente da carga que está sobre as placas do capacitor, isso significa que carga sobre o capacitor também varia com o tempo.
Essa carga pode ser escrita como
Agora, como a corrente é a taxa de variação da carga com o tempo, ou seja, , temos que
já que a capacitância não varia como tempo, uma vez que não depende de nem de . Como
a corrente é dada por
Portanto, a resposta de 11a) é a letra b).
Passo 2
Para resolver a parte 11b) da questão, precisamos da lei de Ampère
em que é a corrente de deslocamento e tem a seguinte expressão
em que o fluxo elétrico é dado por
Passo 3
Vamos utilizar a figura abaixo para tentar visualizar a situação física do problema e também para operarmos com as equações.
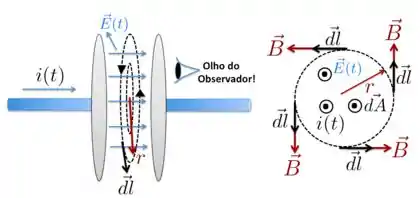
Primeiro, temos uma corrente que aumenta com o tempo cujas cargas vão se armazenando sobre as placas do capacitor. Essas cargas produzem um campo elétrico perpendicular às placas do capacitor, como mostra a figura e também perpendicular à área tracejada de raio . Portanto, esse campo elétrico atravessa uma área e, por isso, podemos falar em fluxo do campo elétrico que varia como tempo.
Agora, se esse fluxo varia no tempo, podemos associar a ele uma corrente de deslocamento. Essa corrente, por sua vez, produz um campo magnético que é tangente à curva fechada de raio . Este campo vai estar no sentido anti-horário visto por um observador em frente à placa da direita, como mostra a figura. Representamos a curva fechada como vista pelo observador à direita. Tanto como estão saindo do plano da página.
Como é sempre paralelo a e tem o mesmo valor em todos os pontos da curva fechada, podemos escrever o lado direito da lei de Ampère como
Passo 4
Agora como fica o fluxo do campo elétrico? Bom, como o campo elétrico tem o mesmo valor em todos os pontos da área em cada instante e é sempre paralelo à área , como mostra a figura, podemos escrever
Igualando essa equação com a última que obtivemos no Passo 3, chegamos a
Portanto, a parte 11b) da questão tem como correto o item b).
Resposta
Parte 11a) letra b
Parte 11b) letra b