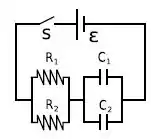
Uma bateria ideal de força eletromotriz está conectada a um circuito composto de dois
resistores e dois capacitores, como mostra o esquema da figura. Inicialmente, a chave S está aberta e os capacitores estão completamente descarregados. Sabe-se que e que .
b) Calcule o valor de i imediatamente depois de a chave S ser fechada. Explique fisicamente por que a corrente possui esse valor.
Passo 1
Olá, tudo tranquilo? Bora resolver essa questão? Agora queremos descobrir o valor da corrente depois da chave S ser fechada. Bom, inicialmente os capacitores estão descarregados, então inicialmente a corrente que passa pelo circuito é aquela que levamos em consideração apenas as resistências. Mas e depois?

Depois os capacitores passam a ser carregados! E no item anterior calculamos a constante de tempo desse circuito!
Calculamos também a corrente em função do tempo! Então a ideia aqui é resgatar de lá o resultado da corrente e aplicar na constante de tempo que achamos!
Mas pode ficar tranquilo, vou fazer passo a passo com você!
 Vamos começar?
Vamos começar?
Passo 2
Vamos resgatar a expressão para a corrente no nosso circuito:
É uma equação de carregamento! Não se esqueça disso! Agora vamos substituir os valores!
Temos duas resistências em paralelo, de modo que a resistência equivalente será:
Da mesma forma, temos dois capacitores em paralelo, de forma que a capacitância equivalente será:
E sabemos que e que , daí
Prontinho!

Ufa, acabou por aqui! #partiu treinar mais?