UFPE- Sem Campus - Física 3-Provas Antigas-P2 - IME2021.2 – Questão 2
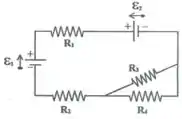
- O módulo e o sentido (horário ou anti-horário) das correntes elétricas em cada resistor.
- A potência dissipada em cada resistor.
- A pot��ncia fornecida ou recebida por cada bateria (explicite para cada bateria isoladamente).
Passo 1
Fala galerinha, tudo tranquilo??? Vamos lá resolver essa questão
A)
Primeiramente, vamos redesenhar a figura para facilitar a resolução e para isso vamos descobrir a resistência equivalente entre . Em seguida vamos descobrir o valor das correntes, uma vez que temos as resistências e as tensões, podemos relacioná-las.(◉ω◉) Se liga:
6V =
Calculando a resistência equivalenteComo as resistências de , que estão em paralelo, temosa resistência equivalente é dada por:
Sabendo que , podemos fazer o somatório das tensões e igualar a zero.
Temos as tensões nos resistores é igual a:
Substituindo que
Substituindo os valores:
Por estar negativa, mostra que está no sentido contrário ao adotado, ou seja, está no sentido anti-horário.
No nó “a”, . Como os resistores são ambos de , .
Como nesse nó a corrente se divide em e , temos:
Também no sentido anti-horário.
Passo 2
B)
Agora temos todas as correntes, assim como as resistências ( ͡° ͜ʖ ͡°)
Que fórmula podemos usar para encontrar a potência em cada resistor? Utilizaremos essa abaixo:
Assim, temos:
Para o resistor 1:
Para o resistor 2:
Para o resistor 3:
Para o resistor 4:
Passo 3
C)
Pessoal, , segundo o texto da questão. Isso quer dizer que a bateria fornece energia, enquanto recebe energia.
Assim:
Negativa porque está recebendo.
Positiva por estar fornecendo.
E assim encerramos essa questão! O que acharam da resolução? Deixe seu feedback
Um abraço e até a próxima!! (/◕ヮ◕)/
Bons Estudos! :)
Resposta
- ,