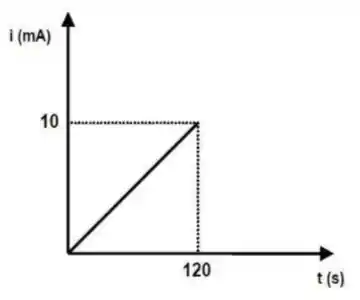
No gráfico abaixo pode-se observar a variação da corrente elétrica em função do tempo através da secção transversal de um condutor. A partir dos dados fornecidos, podemos afirmar que a carga elétrica total que circulou por esta secção. Considere a carga do elétron .
Passo 1
Bom, pra começar, você precisa se lembrar do que é a corrente elétrica, a corrente elétrica é a taxa de variação da carga no tempo, ou seja
Então, resolvendo essa EDO separável, temos
Integrando em ambos os lados
Passo 2
Então, precisamos da função que define a variação da corrente para integrarmos, do gráfico, vemos que a função é uma reta, e a equação da reta é dada por
Temos então que
Substituindo os pontos mostrados, ficamos com
Então, a função é dada por
Passo 3
Agora basta integrarmos
Resposta
Exercícios de Livros Relacionados
Enquanto você está reformando sua garagem, você precisa emendar temporariamente um fio de cobre de 80 m de comprimento e 1,00 mm de diâmetro com um fio de alumínio de 49 m de comprimento, que tem o me
A Figura 20.13 mostra um cone feito de material com resistividade ρ , com a ponta aparada por um plano paralelo à base. As duas faces circulares do corpo têm raios a e b , e forma metalizadas. Supondo
Mostre que a resistência elétrica de uma placa quadrada de espessura fixa, para correntes paralelas a uma de suas arestas, independe do tamanho da placa.
Seguindo o procedimento análogo ao do 20.6P, calcule a constante de tempo de um capacitor esférico preenchido por um dielétrico.
A Figura 20.12 mostra um capacitor cilíndrico preenchido por um material dielétrico de resistividade elétrica ρ e constante dielétrica κ . Uma bateria aplica uma voltagem V ao capacitor.a) Calcule a c