Uma bateria ideal de força eletromotriz está conectada a um circuito composto de dois
resistores e dois capacitores, como mostra o esquema da figura. Inicialmente, a chave S está aberta e os capacitores estão completamente descarregados. Sabe-se que e que .
c) Calcule o valor de i(t) muito tempo depois de a chave S ser fechada. Explique fisicamente por que a corrente possui esse valor.
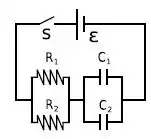
Passo 1
Olá, tudo tranquilo? Bora resolver esse último item dessa questão?
A ideia aqui é a partir da expressão da corrente que encontramos no item anterior, calcular o limite quando
Mas podemos fazer algumas previsões! Temos um circuito com capacitores e resistores, que está inicialmente descarregado. Quando a chave e fechada, a corrente começa a circular e sai de um valor máximo, pois temos a máxima passagem de carga (justamente carregando os capacitores)

Lembrando que a corrente é definida como a quantidade de carga que passa por seção reta do fio por unidade de tempo, quando os capacitores estão carregados a corrente para de passar no ramo onde ele está! Isso porque não temos mais carga passando!

Então a ideia é essa! Aplicar esse conceito de capacitor completamente carregado (é o que acontece no infinito)
 Vamos começar?
Vamos começar?
Passo 2
Do item anterior encontramos uma expressão que dá a corrente em função do tempo nesse circuito
Fazendo o limite de temos
Quando atinge valores muito grandes, o valor de
Cada vez mais se aproxima de zero! Então podemos concluir que a corrente é zero no infinito! E isso corrobora com o que pensamos no passo anterior! Quando capacitores estão bem carregados, não tem mais carga passando, então na malha onde esse capacitor está é como se tivesse um fio cortado, não passa mais corrente ali!
Como nosso circuito tem uma malha só, quando cortamos a parte dos capacitores, é como se fosse um circuito aberto, e por ali não passa corrente!
Beleza? Espero ter ajudado!