Considere as seguintes afirmações:
- As transformações de Galileu são obtidas das transformações de Lorentz no limite .
- A simultaneidade entre dois eventos é relativa ao observador e isso não viola os postulados da relatividade restrita.
- Em princípio, a energia cinética de uma partícula pode ser tão grande quanto se queira.
- Nenhuma afirmativa é verdadeira.
- Apenas é verdadeira.
- Apenas é verdadeira.
- Apenas é verdadeira.
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Todas as afirmativas são verdadeiras.
Passo 1
“As transformações de Galileu são obtidas das transformações de Lorentz no limite .”
VERDADEIRO
Na mecânica clássica, onde usamos as transformações de Galileu, não temos uma velocidade limite para os movimentos. É como se ela fosse infinita.
Como as transformações de Lorentz são uma generalização das de Galileu quando corrigimos apenas isso, elas de fato tem que nos dar as de Galileu no limite .
Agora, menos verbal, e colocando a mão nas equações, as transformações de Lorentz são, para um referencial em movimento uniforme com velocidade em relação a um referencial :
Onde
Se fizermos , teremos que e que , logo:
Que são exatamente as transformações de Galileu.
Passo 2
“A simultaneidade entre dois eventos é relativa ao observador e isso não viola os postulados da relatividade restrita.”
VERDADEIRO
A simultaneidade entre dois eventos ser relativa ao observador é consequência dos postulados da relatividade restrita. Então não tem como ele violar esses postulados, se não teríamos um paradoxo!
De fato, essa relatividade da simultaneidade começa a surgir quando postulamos que a velocidade da luz é a mesma em todos os referenciais inerciais, sem ter nenhum privilegiado.
Passo 3
“Em princípio, a energia cinética de uma partícula pode ser tão grande quanto se queira.”
VERDADEIRO
Na relatividade, a energia cinética de uma partícula é dada por
Onde é a massa de repouso da partícula, sendo assim uma constante que só depende da natureza dela (e se ela vai perder ou não massa).
O fator de Lorentz é dado por:
A medida que vai ficando cada vez mais perto de , temos que vai tendendo ao infinito. O gráfico do fator de Lorentz fica mais ou menos assim:
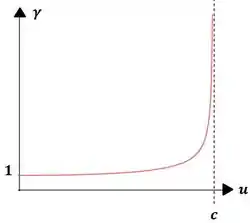
Isso significa que podemos fazer ser tão grande quanto quisermos fazendo se aproximar de . Então a energia cinética também pode ser tão grande quanto quisermos, visto que o resto dos termos são constantes do problema!
A resposta então é a letra , todas as afirmativas são verdadeiras.
Resposta
Letra
Todas as afirmativas são verdadeiras.