UFSC, Araranguá, Física 1, P3 - 2021.2, Questão 1
Um isótopo do elemento polônio (símbolo 210Po), com massa igual a , pode decair e dar origem a uma partícula (que é na verdade um núcleo do átomo de hélio) com massa de , e a um isótopo do chumbo (símbolo 206Pb) de massa :
210Po 206Pb
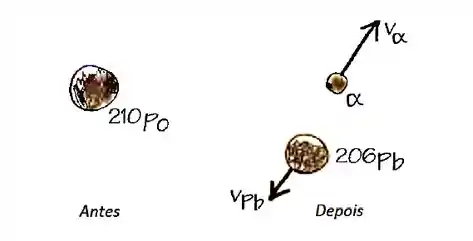
Nesse processo de decaimento, os produtos (206Pb e ) possuem, somados, uma energia cinética de se o átomo de polônio estiver em repouso, que é a situação considerada aqui. Quais as velocidades da partícula e do isótopo 206Pb depois do processo de decaimento? Observe a figura abaixo.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu um processo de decaimento do polônio que libera energia cinética e faz um átomo e uma partícula entrarem em movimento. A figura mostra que cada velocidade aponta para um lado, mas a velocidade inicial do polônio é zero. Ele nos dá a massa de cada elemento, a energia cinética final, e pede pra gente calcular a velocidade partícula e do isótopo 206Pb depois do processo de decaimento.
Beleza, vamos analisar o processo. Como a velocidade inicial do polônio é zero, significa que sua energia cinética inicial, , também é zero. E nós sabemos que a energia cinética final é . Como a energia cinética é dada por:
Nós podemos fazer o balanço de energia para determinar as velocidades finais:
Onde e são a massa e a velocidade final do chumbo e e a massa e a velocidade final da partícula . Vamos substituir os dados do enunciado para encontrar cada velocidade.
Vamos lá!
Passo 2
Nós temos:
Antes de substituir isso na equação de energia, nós precisamos lembrar que, como a energia cinética inicial é zero, a quantidade de movimento inicial também é zero, e dessa forma, temos no final:
Onde é a quantidade de movimento do chumbo e a quantidade de movimento da partícula . Sabendo que , temos:
Logo,
Substituindo na equação:
Isolando , temos:
Substituindo os dados do enunciado:
Substituindo esse resultado na nossa equação do movimento, temos:
Prontinho, galera! Até a próxima! 😉