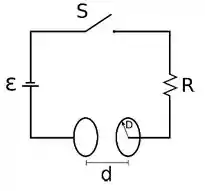
Um circuito é formado por uma chave , uma fonte ideal , um resistor de resistência e um capacitor com constante dielétrica . O capacitor é formado por duas placas circulares e paralelas com raio e separadas por uma distância . No instante a chave é fechada. Suponha que o campo elétrico entre as placas é uniforme.
a) Calcule a corrente de deslocamento no capacitor.
b) Calcule a taxa de variação no tempo do campo elétrico, , no capacitor.
c) Qual é o módulo do campo magnético no interior do capacitor no instante a uma distância radial medida a partir do centro do capacitor.
Passo 1
a) A corrente de deslocamento do capacitor é dada por
No caso, a tensão aplicada é e a capacitância é , então:
Passo 2
b) Partindo da lei de Ampére, a gente chega que a taxa de variação do campo elétrico é dada por
Sabendo que , vamos substituir as expressões:
Passo 3
c) O campo magnético presente entre as placas vai ser dado por
Substituindo as expressões:
Resposta
a)
b)
c)