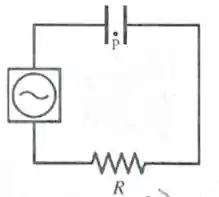
Um capacitor está conectado a um resistor e a uma fonte de voltagem alternada como mostrado na figura. A fonte fornece uma fem dada por . As placas do capacitor são discos de raio . O ponto está entre duas placas, equidistante destas e a uma distância do centro do eixo de simetria. De acordo com a teoria eletromagnética, no ponto
- Não há campo magnético porque não existe carga se movendo entre as placas.
- Existe um campo magnético constante.
- Existe uma corrente de elétrons fluindo.
- Existe um campo elétrico constante no tempo.
- Existe um campo magnético variável no tempo.
Passo 1
Aqui precisamos ter em mente que a teoria eletromagnética diz que um campo magnético variável no tempo gera um campo elétrico e também que que um campo elétrico variável no tempo produz um campo magnético.
O potencial dependente do tempo envia cargas que vão se acumulando sobre as placas do capacitor e, por essa razão, a carga do capacitor varia no tempo também. Consequentemente, o campo elétrico produzido por essas cargas e que está dentro das placas também depende do tempo.
Se o campo elétrico é variável e alterna no tempo na região entre as placas, então, também haverá um campo magnético na região onde está o ponto .
Passo 2
Assim pela correção e Maxwell temos a chamada corrente de deslocamento. Não é uma corrente de elétrons, no sentido convencional, e sim uma corrente pois gera um campo magnético circular na placa (o que se assemelha – e muito – com o campo magnético produzido por um fio percorrido por corrente, aquela corrente da lei de Ampère)
E essa corrente é que gera um campo magnético de padrão circular (e em todos os pontos a uma mesma distância do centro da placa, é constante), então por convenção chama-se corrente, mas para diferenciar, colocamos um ‘sobrenome’ nela: corrente de deslocamento
De deslocamento porque é o que possibilita o carregamento do capacitor! Beleza?
Obs: aqui é o fluxo elétrico, pois é essa quantidade que precisa ser variável no tempo! (como a área não muda, o campo obrigatoriamente precisa mudar. Alguma componente do fluxo precisa variar no tempo para que tenhamos corrente de deslocamento, ok?)
Passo 3
Sendo assim, um campo elétrico variável no tempo gera um campo magnético constante, e a alternativa correta é (b)
Te ajudei? Responde aí!
Resposta
Letra b.