Exercícios Resolvidos de Função de Probabilidade & Função de Distribuição Acumulada
Ver TeoriaEnunciado
Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Considera uma v.a. discreta com a seguinte função de probabilidade:
- Determine a constante para que seja uma função de probabilidade da variável aleatória .
- Encontre a função de distribuição de probabilidade acumulada de . Plotar em gráfico esta função acumulada.
Passo 1
a)
Lembre-se sempre que a integral está para a função de probabilidade contínua, assim como o somatório está para a função de probabilidade discreta!
Aqui temos que lembrar as condições para uma função ser função de densidade:
Para ser sempre positiva, já podemos ter certeza que tem que ser positivo. Mas para saber seu valor exato, vamos resolver esse somatório:
Tá indo de a por que esses aí são os valores mínimos e máximos que nosso pode ser. Abrindo o somatório:
Mas acabamos de ver que isso aí tem que ser igual a , fazendo essa igualdade:
Passo 2
b)
Para achar a FDA, podemos lembrar que:
Podemos calculá-la para cada um dos nossos valores de :
Passo 3
Temos que plotar num gráfico então uma função que comece no e termine no e vá subindo em degraus conforme os valores encontrados:
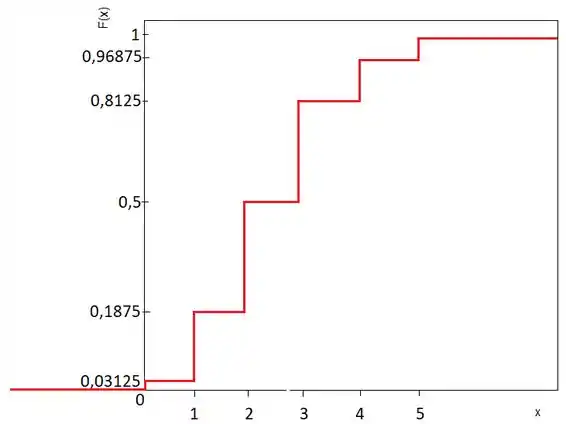
Resposta
a)
b)
